
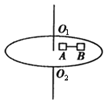
 ��ͼ��ʾ������ת����ˮƽԲ���Ϸ��������ֱ�Ϊ2kg��3kg��С����A��B��A��B����ϸ���ذ뾶�������������ǵ�ת��ľ���ֱ�ΪRA=0.2m��RB=0.3m��A��B�����������Ħ������Ϊ������0.4����gȡ10m/s2���ּ��仺��������Բ�̵Ľ��ٶȣ�������˵����ȷ���ǣ�������
��ͼ��ʾ������ת����ˮƽԲ���Ϸ��������ֱ�Ϊ2kg��3kg��С����A��B��A��B����ϸ���ذ뾶�������������ǵ�ת��ľ���ֱ�ΪRA=0.2m��RB=0.3m��A��B�����������Ħ������Ϊ������0.4����gȡ10m/s2���ּ��仺��������Բ�̵Ľ��ٶȣ�������˵����ȷ���ǣ�������| A�� | С����A�ﵽ���Ħ����ʱ��B�ܵ���Ħ������СΪ12N | |
| B�� | ��Aǡ�ôﵽ���Ħ����ʱ��Բ�̵Ľ��ٶ�Ϊ4rad/s | |
| C�� | ϸ���Ͽ�ʼ�е���ʱ��Բ�̵Ľ��ٶ�Ϊ$\frac{2\sqrt{30}}{3}$rad/s | |
| D�� | ijʱ�̼���ϸ�ߣ�A���������˶���B���������˶� |
���� ������ԭ�̵Ľ��ٶȣ�B�ȴﵽ���Ħ����������A�ﵽ���Ħ����ʱ��B��Ħ����Ҳ���Aǡ�ôﵽ���Ħ����ʱ����A��B����������ţ�ٵڶ����ɷֱ���ʽ�������ٶȴ�С��ϸ���Ͽ�ʼ�е���ʱ��B���������Ħ��������ţ�ٵڶ����ɿ������ٶȣ�ijʱ�̼���ϸ�ߣ���������ǰ�������仯�ɷ������������˶������
��� �⣺A��������ԭ�̵Ľ��ٶȣ�B�ȴﵽ���Ħ����������A�ﵽ���Ħ����ʱ��B��Ħ����Ҳ����СΪ��FB=kmBg=12N����Aѡ����ȷ��
B����Aǡ�ôﵽ���Ħ����ʱ��Բ�̵Ľ��ٶ�Ϊ�أ���ʱϸ���ϵ�����ΪT������ţ�ٵڶ����ɣ�
��A��$k{m}_{A}g-T={m}_{A}{��}^{2}{r}_{A}$
��B��$T+k{m}_{B}g={m}_{B}{��}^{2}{r}_{B}$
�����ɽ�ģ�$��=\frac{10\sqrt{2}}{13}rad/s$����Bѡ�����
C����ϸ���Ͽ�ʼ�е���ʱ����ʱB�����ܵ����Ħ��������ţ�ٵڶ����ɣ�$k{m}_{B}g={m}_{B}{{��}_{1}}^{2}{r}_{B}$���ɵã�${��}_{1}=\frac{2\sqrt{30}}{3}rad/s$����Cѡ����ȷ��
D��ijʱ�̼���ϸ�ߣ�A����Ħ������С����ԭ�̼�����Բ���˶���B������ϸ�����������Ħ�����������ṩ���������������˶�����Dѡ�����
��ѡ��AC
���� �����е����ٶȷ����仯ʱ��һ��Ҫ�������AB�������������ı仯�����Բ��ü���û��ϸ�߷������Ħ�����ij���ʱ�̣���������������ʽ���з������㣮


 ��������ϵ�д�
��������ϵ�д� ���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
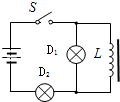 ��ͼ��ʾ��L���Ը��㹻�����Ȧ����ֱ�����費�ƣ�D1��D2����ȫ��ͬ�ĵ��ݣ���S�պϣ��ȵ��������ȶ����ٶϿ�S����S�պ�ʱ��Ͽ�ʱ�����з�����ȷ���ǣ�������
��ͼ��ʾ��L���Ը��㹻�����Ȧ����ֱ�����費�ƣ�D1��D2����ȫ��ͬ�ĵ��ݣ���S�պϣ��ȵ��������ȶ����ٶϿ�S����S�պ�ʱ��Ͽ�ʱ�����з�����ȷ���ǣ�������| A�� | S�պ�ʱ��D2������D1���� | |
| B�� | S�պ�ʱ��D1��D2ͬʱ����Ȼ��D1Ϩ�� | |
| C�� | S�Ͽ�ʱ��D2����Ϩ��D1Ҫ��һ����Ϩ�� | |
| D�� | S�Ͽ�ʱ��D1��D2һ����Ϩ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
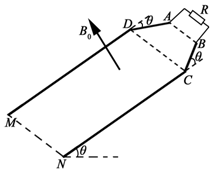 ��ͼ��ʾ����������ADM��BCN�̶������Ϊ��=30���б���ϣ�����AB��CD�䵼��⻬��ABCDΪ�������Σ�AB��ΪL��CD��Ϊ2L��CB��NC�н�Ϊ�ȣ�����CD��MN��Ϊ�㹻���Ҵֲڵ�ƽ�е��죮���춥�˽�����ֵΪR�Ķ�ֵ���裬�ռ��г����Ÿ�Ӧǿ�ȴ�СΪB0������ֱб�����ϵ���ǿ�ų����ִ�AB���ɾ�ֹ�ͷ�һ����Ϊm����Ϊ2L�ĵ������������ڹ⻬�������˶�ʱ���ٶȲ�Ϊ�㣬�����ʼ��ˮƽ���뵼��Ӵ����ã���֪�������ֲڵ����Ķ�Ħ�������̣�$\frac{\sqrt{3}}{3}$���������������費�ƣ��������ٶ�Ϊg��������˵������ȷ���ǣ�������
��ͼ��ʾ����������ADM��BCN�̶������Ϊ��=30���б���ϣ�����AB��CD�䵼��⻬��ABCDΪ�������Σ�AB��ΪL��CD��Ϊ2L��CB��NC�н�Ϊ�ȣ�����CD��MN��Ϊ�㹻���Ҵֲڵ�ƽ�е��죮���춥�˽�����ֵΪR�Ķ�ֵ���裬�ռ��г����Ÿ�Ӧǿ�ȴ�СΪB0������ֱб�����ϵ���ǿ�ų����ִ�AB���ɾ�ֹ�ͷ�һ����Ϊm����Ϊ2L�ĵ������������ڹ⻬�������˶�ʱ���ٶȲ�Ϊ�㣬�����ʼ��ˮƽ���뵼��Ӵ����ã���֪�������ֲڵ����Ķ�Ħ�������̣�$\frac{\sqrt{3}}{3}$���������������費�ƣ��������ٶ�Ϊg��������˵������ȷ���ǣ�������| A�� | ������ڹ⻬�����������ٶ�����ļ����˶� | |
| B�� | ������ڹ⻬�������˶����̣�ͨ����ֵ����ĵ����Ϊ$\frac{3\sqrt{3}{B}_{0}{L}^{2}}{4R}$ | |
| C�� | ������ڴֲڵ�����һ���������ٶȼ�С�ļ����˶�������������˶� | |
| D�� | ��=$\frac{2\sqrt{3}}{9}$ʱ��������������ٶȴ�СΪ$\frac{mgR}{24{{B}_{0}}^{2}{L}^{2}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ��ʾ�����б���ϵ�Q�����ɻ��£�ͨ���ֲڵľ�ֹˮƽ���ʹ����䵽�����ϵ�P�㣮�����ʹ�˳ʱ��ת�����ٰ����ŵ�Q�����ɻ��£���ô��������
��ͼ��ʾ�����б���ϵ�Q�����ɻ��£�ͨ���ֲڵľ�ֹˮƽ���ʹ����䵽�����ϵ�P�㣮�����ʹ�˳ʱ��ת�����ٰ����ŵ�Q�����ɻ��£���ô��������| A�� | ����������P�� | B�� | ����������P����� | ||
| C�� | ������������P���ұ� | D�� | �������䵽P���ұ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ����Բ���˶� | B�� | ƽ���˶� | C�� | �ȱ���ֱ���˶� | D�� | �ȱ��������˶� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | v1��=-2m/s��v2��=3m/s | B�� | v1��=3m/s��v2��=0.5m/s | ||
| C�� | v1��=1m/s��v2��=3m/s | D�� | v1��=-1m/s��v2��=2.5m/s |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
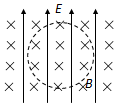 ��ͼ��ʾ��һ�����ʵ��ڴ�ֱֽ���������ǿ�ų�B����ֱ���ϵ���ǿ�糡E�Ŀռ�����ֱ���ڵ�����Բ���˶���������
��ͼ��ʾ��һ�����ʵ��ڴ�ֱֽ���������ǿ�ų�B����ֱ���ϵ���ǿ�糡E�Ŀռ�����ֱ���ڵ�����Բ���˶���������| A�� | �ʵ�һ�������� | B�� | �ʵ���˳ʱ���˶� | ||
| C�� | �ʵ������һ�����Բ��� | D�� | �ʵ���˶�����Ϊv=E/B |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
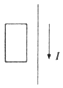 ��ͼ��ʾ��һͨ�е���I��ֱ���ߺ�һ���ε��߿�ƽ�з�����ͬһƽ���ϣ����߿����ĸ������˶�ʱ���Ż��ܵ����ҵĺ�����������
��ͼ��ʾ��һͨ�е���I��ֱ���ߺ�һ���ε��߿�ƽ�з�����ͬһƽ���ϣ����߿����ĸ������˶�ʱ���Ż��ܵ����ҵĺ�����������| A�� | ���� | B�� | ���� | C�� | ���� | D�� | ���� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
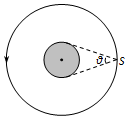 ��ͼ��ʾ��ij����S�Ƶ���������ΪT������Բ���˶��������������S���Ž�Ϊ�ȣ�������Ϊ�����ֲ����ȵ����壬������������ٶ�Ϊg����������ΪG������˵����ȷ���ǣ�������
��ͼ��ʾ��ij����S�Ƶ���������ΪT������Բ���˶��������������S���Ž�Ϊ�ȣ�������Ϊ�����ֲ����ȵ����壬������������ٶ�Ϊg����������ΪG������˵����ȷ���ǣ�������| A�� | ����S�Ĺ���뾶r=$\frac{{T}^{2}gsi{n}^{2}��}{4{��}^{2}}$ | |
| B�� | ����S���ٶȴ�Сv=$\frac{Tg}{2��}$sin2$\frac{��}{2}$ | |
| C�� | ������ܶ�Ϊ$\frac{3��}{G{T}^{2}si{n}^{3}\frac{��}{2}}$ | |
| D�� | ����ĵ�һ�����ٶȴ�СΪ$\frac{Tg}{2��}$sin$\frac{��}{2}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com