
 ��ͼ��ʾ���ڹ⻬��Ե��ˮƽ���ϣ��ó�Ϊ2L�ľ�Ե�������������Ϊm�Ĵ���С��A��B��A��Ĵ�����Ϊ+3q��B��Ĵ�����Ϊ-4q���������һ����ϵͳ������MN��PQƽ�������3L����ʼʱA��B�ֱ�ֹ������MN�����࣬����MNǡΪAB�������ߵĴ�ֱƽ���ߣ�����С��Ϊ�ʵ㣬������˵�������������MN��PQ�����ˮƽ���ҵĵ糡ǿ��ΪE����ǿ�糡������
��ͼ��ʾ���ڹ⻬��Ե��ˮƽ���ϣ��ó�Ϊ2L�ľ�Ե�������������Ϊm�Ĵ���С��A��B��A��Ĵ�����Ϊ+3q��B��Ĵ�����Ϊ-4q���������һ����ϵͳ������MN��PQƽ�������3L����ʼʱA��B�ֱ�ֹ������MN�����࣬����MNǡΪAB�������ߵĴ�ֱƽ���ߣ�����С��Ϊ�ʵ㣬������˵�������������MN��PQ�����ˮƽ���ҵĵ糡ǿ��ΪE����ǿ�糡���������� ��1����ϵͳ���ö��ܶ��������ݶ��ܶ������B��ս���糡ʱ������ϵͳ���ٶȴ�С��
��2������ϵͳ�����������Σ���B�����糡ǰ������ϵͳ�ڵ糡�С�A����糡�����ݶ��ܶ������A���뿪PQ�����λ�ƣ��Ӷ��������ϵͳ�����˶��������룮����B���ڵ糡���˶���λ�ƣ�����糡�����Ĺ����Ӷ�ȷ��B������ܵı仯����
��3�������˶�ѧ��ʽ��ţ�ٵڶ����ɷֱ��������ϵͳB�����糡ǰ���ȼ���ֱ���˶���ʱ�䣬����ϵͳ�ڵ糡�����ȼ���ֱ���˶���ʱ�䣬A����糡����ϵͳ���ȼ���ֱ���˶���ʱ�䣬�Ӷ��������ϵͳ�Ӿ�ֹ��ʼ�����˶��ٴ��ٶ�Ϊ���ʱ�䣬����ϵͳ���˶�����Ϊ��ʱ���2����
��� �⣺��1����B��ս���糡ʱ����ϵͳ���Ϊv1���ɶ��ܶ����ã�
3qEL=$\frac{1}{2}•2m{{v}_{1}}^{2}$��
��ã�${v}_{1}=\sqrt{\frac{3qEL}{m}}$��
��2������ϵͳ�����˶������Σ�B�����糡ǰ������ϵͳ�ڵ糡�С�A����糡����A���뿪PQ�����λ��Ϊx���ɶ��ܶ����ã�
3qEL-qEL-4qEx=0
���x=$\frac{L}{2}$�������ϵͳ�����˶���������Ϊ��s��=$\frac{5L}{2}$��
B��Ӹս���糡������ϵͳ�ӿ�ʼ�˶����ٶȵ�һ��Ϊ��ʱλ��Ϊ$\frac{3L}{2}$��
��糡������$W=-4qE•\frac{3}{2}L+3qE•2L$=0��������ܵı仯����Ep=0��
��3�������˶������Σ�ȡ����Ϊ������
��һ�μ��٣�${a}_{1}=\frac{3qE}{2m}$��
��${t}_{1}=\frac{{v}_{1}}{{a}_{1}}=\sqrt{\frac{4mL}{3qE}}$��
�ڶ��μ��٣�${a}_{2}=\frac{-qE}{2m}$��
��A����糡���ٶ�Ϊv2���ɶ��ܶ����ã�$-qEL=\frac{1}{2}2m{{��v}_{2}}^{2}-{v}_{1}��^{2}$��
��ã�v2=$\sqrt{\frac{2qEL}{m}}$��
��${t}_{2}=\frac{{v}_{2}-{v}_{1}}{{a}_{2}}$=$2��\sqrt{3}-\sqrt{2}��\sqrt{\frac{mL}{qE}}$��
�������ټ���������ٶ�a3��ʱ��t3Ϊ��${a}_{3}=\frac{-4qE}{2m}=\frac{-2qE}{m}$��${t}_{3}=\frac{0-{v}_{2}}{{a}_{3}}$=$\sqrt{\frac{mL}{2qE}}$��
���Դ���ϵͳ�˶�������Ϊ��T=2��t1+t2+t3��=2$��\frac{8\sqrt{3}}{3}-\frac{3\sqrt{2}}{2}��\sqrt{\frac{mL}{qE}}$��
�𣺣�1��B��ս���糡ʱ������ϵͳ���ٶȴ�СΪ$\sqrt{\frac{3qEL}{m}}$��
��2������ϵͳ�����˶���������Ϊ$\frac{5L}{2}$���˹�����B������ܵı仯��Ϊ0��
��3������ϵͳ�˶�������Ϊ2$��\frac{8\sqrt{3}}{3}-\frac{3\sqrt{2}}{2}��\sqrt{\frac{mL}{qE}}$��
���� �������Ĺؼ��������ϵͳ�����������е��˶���������ţ�ٵڶ����ɡ����ܶ������˶�ѧ��ʽ�ۺ���⣮


 ����ѧ���ʱѧ����ϵ�д�
����ѧ���ʱѧ����ϵ�д� �ʰ�Ӣ��ͬ����ϰ��ϵ�д�
�ʰ�Ӣ��ͬ����ϰ��ϵ�д� ѧϰʵ����ϵ�д�
ѧϰʵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �٢� | B�� | �٢� | C�� | �ڢ� | D�� | �ۢ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | �˽����������ЧֵΪ3A�����ֵΪ 3$\sqrt{2}$A | |
| B�� | �˽����������ЧֵΪ3$\sqrt{2}$A�����ֵΪ6A | |
| C�� | �������˵Ľ��������ѹ����ЧֵΪ300V�����ֵΪ300$\sqrt{2}$V | |
| D�� | �������˵Ľ��������ѹ����ЧֵΪ300$\sqrt{2}$V�����ֵΪ600V |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | �������������Ĺ����������������ܵ����� | |
| B�� | �������������Ĺ��������嶯�ܵ����� | |
| C�� | �糡���Ե�����Ĺ����ڵ�ɵ����ܵļ��� | |
| D�� | �������͵���������������������֮�͵��������е�ܵļ��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
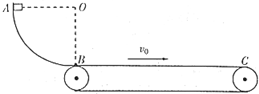 ��ͼ��ʾ��һ����Ϊm=2kg�Ļ���Ӱ뾶ΪR=0.2m�Ĺ⻬�ķ�֮һԲ������Ķ���A���ɾ�ֹ���£�A���Բ����Ӧ��Բ��O��ȸߣ�Բ���ĵ�B��ˮƽ���ʹ�ƽ����ӣ���֪���ʹ��������е��ٶ�Ϊv0=4m/s��B�㵽���ʹ��Ҷ�C��ľ���ΪL=2m�������黬�����ʹ����Ҷ�Cʱ�����ٶ�ǡ���봫�ʹ����ٶ���ͬ����g=10m/s2����
��ͼ��ʾ��һ����Ϊm=2kg�Ļ���Ӱ뾶ΪR=0.2m�Ĺ⻬�ķ�֮һԲ������Ķ���A���ɾ�ֹ���£�A���Բ����Ӧ��Բ��O��ȸߣ�Բ���ĵ�B��ˮƽ���ʹ�ƽ����ӣ���֪���ʹ��������е��ٶ�Ϊv0=4m/s��B�㵽���ʹ��Ҷ�C��ľ���ΪL=2m�������黬�����ʹ����Ҷ�Cʱ�����ٶ�ǡ���봫�ʹ����ٶ���ͬ����g=10m/s2�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ��һ������Ϊm=l kg�����徲ֹ��ˮƽ���ϣ�������ˮƽ��Ķ�Ħ������Ϊ0.5������ˮƽ���������ʩ��F=10N��������gȡ10m/s2����
��ͼ��ʾ��һ������Ϊm=l kg�����徲ֹ��ˮƽ���ϣ�������ˮƽ��Ķ�Ħ������Ϊ0.5������ˮƽ���������ʩ��F=10N��������gȡ10m/s2�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ��һ������ϸ������ϵ��Ϊk������һ�˹̶�����һ�˴���һ�⻬С��Oϵסһ����Ϊm�Ļ��飬�������ˮƽ�����ϣ���ϸ����ֱʱ��С��O������ľ���ǡΪ����ϸ��ԭ����С��O��ˮƽ����ľ���Ϊh��h��$\frac{mg}{k}$����������ˮƽ�����Ķ�Ħ������Ϊ�̣������龲ֹʱ���ɴ���ʲô����λ�ã�
��ͼ��ʾ��һ������ϸ������ϵ��Ϊk������һ�˹̶�����һ�˴���һ�⻬С��Oϵסһ����Ϊm�Ļ��飬�������ˮƽ�����ϣ���ϸ����ֱʱ��С��O������ľ���ǡΪ����ϸ��ԭ����С��O��ˮƽ����ľ���Ϊh��h��$\frac{mg}{k}$����������ˮƽ�����Ķ�Ħ������Ϊ�̣������龲ֹʱ���ɴ���ʲô����λ�ã��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
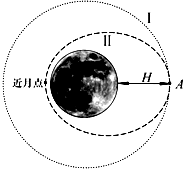 �ҹ���2013��12�·����ˡ��϶����š����ǣ��������ھ��������H���Ļ��¹������������Բ���˶��������е�����ΪT������϶������ڸù����A���ȡ��ʩ���������µ�߶�Ϊh����Բ������ϣ���ͼ��ʾ������R��ʾ����İ뾶������������ת����������ǵ�Ӱ�죮�������ж���ȷ���ǣ�������
�ҹ���2013��12�·����ˡ��϶����š����ǣ��������ھ��������H���Ļ��¹������������Բ���˶��������е�����ΪT������϶������ڸù����A���ȡ��ʩ���������µ�߶�Ϊh����Բ������ϣ���ͼ��ʾ������R��ʾ����İ뾶������������ת����������ǵ�Ӱ�죮�������ж���ȷ���ǣ�������| A�� | ���������Ϊ$\frac{4{��}^{2}��R+H��^{3}}{G{T}^{2}}$ | |
| B�� | ����ĵ�һ�����ٶ�Ϊ$\frac{2��\sqrt{R��R+h��^{3}}}{TR}$ | |
| C�� | ���϶����š��ڻ��¹����������ٲ��ܽ�����Բ����� | |
| D�� | ���϶����š���ͼ����Բ������ϵ�����Ϊ$\sqrt{\frac{��2R+H+h��^{3}}{8��R+H��^{3}}}$T |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com