
设某物质的密度为ρ,其摩尔质量为M,阿伏加德罗常数为NA,已知这种物质的样品的质量为m,则下列表示微观量的式子中正确的是( )
A.该样品物质中含有的分子数为![]() NA
NA
B.该样品物质中每个分子质量为![]()
C.若将该物质分子看成是球体,则每个分子的直径为
D.若将该物质分子看成是正立方体,则相邻两个分子间的距离为![]()
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:高中物理 来源: 题型:
| 2 |
|
| 4 |
| 3 |
查看答案和解析>>
科目:高中物理 来源: 题型:
|
查看答案和解析>>
科目:高中物理 来源: 题型:
A、该样品物质中含有的分子数为
| |||||
B、该样品物质中每个分子的质量为
| |||||
C、若将该样品物质分子看成球体,则每个分子的直径为
| |||||
D、若将该样品物质分子看成立方体,则相邻两个分子间的距离为
|
查看答案和解析>>
科目:高中物理 来源: 题型:
A.该样品物质中含有的分子数为![]() NA
NA
B.该样品物质中每个分子质量为![]()
C.若将该物质分子看成是球体,则每个分子的直径为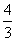
D.若将该物质分子看成是正立方体,则相邻两个分子间的距离为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com