
 ��ͼ��һ�ֹ���-ʯĥ������ĥ�̶̹�������ĥ�̿��ƹ����ĵ���ֱת�ᣬ���Ƹ˴�������ˮƽ����ת����������ĥ��ֱ��ΪD������Ϊm�Ҿ��ȷֲ���ĥ�̼䶯Ħ������Ϊ�̣����Ƹ��������������Խ��ٶȦ�����ת����ĥ��ת��һ�ܣ������˷�ĥ�̼�Ħ��������ΪW��������
��ͼ��һ�ֹ���-ʯĥ������ĥ�̶̹�������ĥ�̿��ƹ����ĵ���ֱת�ᣬ���Ƹ˴�������ˮƽ����ת����������ĥ��ֱ��ΪD������Ϊm�Ҿ��ȷֲ���ĥ�̼䶯Ħ������Ϊ�̣����Ƹ��������������Խ��ٶȦ�����ת����ĥ��ת��һ�ܣ������˷�ĥ�̼�Ħ��������ΪW��������| A�� | ĥ�̱�Ե�����ٶ�Ϊ$\frac{��D}{2}$ | |
| B�� | ĥ�̱�Ե�����ٶ�Ϊ��D | |
| C�� | Ħ�����ĵ�Ч���õ���ת�����Ϊ$\frac{W}{�Ц�mg}$ | |
| D�� | Ħ�����ĵ�Ч���õ���ת�����Ϊ$\frac{W}{2�Ц�mg}$ |

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ʯ�����䵽�������ʱ�� | B�� | ʯ�����ʱ��˲ʱ�ٶ� | ||
| C�� | ʯ�������һ���ڵ�λ�� | D�� | ʯ�������һ��ʱ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
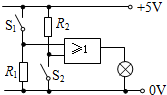
| A�� | Sl��S2���Ͽ�ʱ���ݲ����� | B�� | Sl��S2���պ�ʱ���ݷ��� | ||
| C�� | Sl�Ͽ���S2�պ�ʱ���ݷ��� | D�� | Sl�պϣ�S2�Ͽ�ʱ���ݲ����� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��������Ϊm������С��A��B�̶������120��ǵľ�Ե������ˣ�OA��OB�ij��Ⱦ�Ϊl�����ƹ�O������ֽ�洹ֱ��ˮƽ����Ħ��ת���������������ƣ���A������磬B������磬������Ϊq��������ֱ���µ���ǿ�糡�У���ǿE=$\frac{mg}{3q}$����ʼʱ����OB����ֱ����ļнǦ�=60�㣮
��ͼ��������Ϊm������С��A��B�̶������120��ǵľ�Ե������ˣ�OA��OB�ij��Ⱦ�Ϊl�����ƹ�O������ֽ�洹ֱ��ˮƽ����Ħ��ת���������������ƣ���A������磬B������磬������Ϊq��������ֱ���µ���ǿ�糡�У���ǿE=$\frac{mg}{3q}$����ʼʱ����OB����ֱ����ļнǦ�=60�㣮�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����

| A�� | ������������ | B�� | �����ң������� | C�� | ʼ������ | D�� | ʼ������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ij��ȤС��������ͼa��ʾʵ��װ�ò��������ٶȣ���б������з������ɸ�С���պϿ���K���������ס��1��С���ֶ��û����Խ���ƬM��M�봥ͷ˲��ֿ�����1��С��ʼ���䣬MѸ�ٻָ������������ס��2��С����1��С��ײ��M ʱ��M�봥ͷ�ֿ�����2��С��ʼ���䡭���������Ϳɲ��n��С���������ʱ��T��
ij��ȤС��������ͼa��ʾʵ��װ�ò��������ٶȣ���б������з������ɸ�С���պϿ���K���������ס��1��С���ֶ��û����Խ���ƬM��M�봥ͷ˲��ֿ�����1��С��ʼ���䣬MѸ�ٻָ������������ס��2��С����1��С��ײ��M ʱ��M�봥ͷ�ֿ�����2��С��ʼ���䡭���������Ϳɲ��n��С���������ʱ��T���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
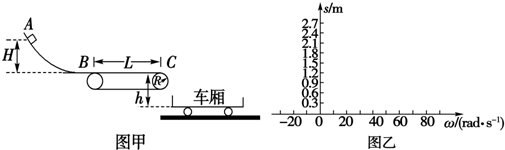
 ��ͼ��ʾ�����δ�����ֹ��ˮƽ�ֲ������ϣ��������Ϸ��̶�-����ֱ���ߣ�������ͨ������ֱֽ������������δ�����ֱ���ĵ�������ͻȻ�������������Ա��־�ֹ��������ܵ���֧����N��Ħ����f��α仯��������
��ͼ��ʾ�����δ�����ֹ��ˮƽ�ֲ������ϣ��������Ϸ��̶�-����ֱ���ߣ�������ͨ������ֱֽ������������δ�����ֱ���ĵ�������ͻȻ�������������Ա��־�ֹ��������ܵ���֧����N��Ħ����f��α仯��������| A�� | N��С��f��С | B�� | N���f��� | C�� | N���f��С | D�� | N��С��f���� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
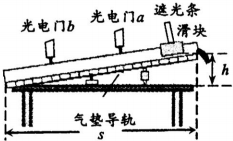 ijͬѧ��ͼʾװ����֤��е���غ㶨�ɣ��Ƚ����浼����б���ã��ÿ̶ȳ߷ֱ����̶��ڵ����ϵ����������a��b����֮��ľ���L���������˵�ˮƽ����s�����˵ĸ߶Ȳ�h�����������α꿨�߲���������ڹ����Ŀ���d��
ijͬѧ��ͼʾװ����֤��е���غ㶨�ɣ��Ƚ����浼����б���ã��ÿ̶ȳ߷ֱ����̶��ڵ����ϵ����������a��b����֮��ľ���L���������˵�ˮƽ����s�����˵ĸ߶Ȳ�h�����������α꿨�߲���������ڹ����Ŀ���d���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com