
 ��ͼ��һ��ֱ��ֽ�����ǿ�ų��ֲ���ֱ������ϵ�ĵ������������ڣ���һ��ǿ�糡�ֲ��ڵڶ��������������ڣ���һ�������糡�ʹų���һ����Ϊm�������Ϊ+q�Ĵ����͵Σ���y���ϵ�M��ˮƽ�����׳�������N������������ǡ��������Բ���˶����͵ξ�x���ϵ�N���P������ֻص�M�㣬��OM=L��ON=2L����ͼ��ʾ����
��ͼ��һ��ֱ��ֽ�����ǿ�ų��ֲ���ֱ������ϵ�ĵ������������ڣ���һ��ǿ�糡�ֲ��ڵڶ��������������ڣ���һ�������糡�ʹų���һ����Ϊm�������Ϊ+q�Ĵ����͵Σ���y���ϵ�M��ˮƽ�����׳�������N������������ǡ��������Բ���˶����͵ξ�x���ϵ�N���P������ֻص�M�㣬��OM=L��ON=2L����ͼ��ʾ�������� ��1���͵ν����������ǡ��������Բ���˶����糡��������ƽ�⣬��ƽ��������⣮
��2���͵δ�M��N����ƽ���˶������ݷ�λ�ƹ�ʽ���ٶȵĺϳ�����͵ε���N��ʱ�ٶȴ�С�ͷ���
��3���������⻭���͵ε��˶��켣������켣�뾶���������������ṩ�������������ǿ�ų��ĴŸ�Ӧǿ�ȵĴ�С���жϴų��ķ���
��4���ֶ����ʱ�䣬������ʱ�䣮
���  �⣺��1���͵ν����������ǡ��������Բ���˶����糡������������ƽ�⣬��糡����ֱ���ϣ��糡ǿ�ȷ�����ֱ���ϣ�
�⣺��1���͵ν����������ǡ��������Բ���˶����糡������������ƽ�⣬��糡����ֱ���ϣ��糡ǿ�ȷ�����ֱ���ϣ�
���� mg=qE���� E=$\frac{mg}{q}$
��2���͵δ�M��N����ƽ���˶������͵���M����ٶ�Ϊv0������N��ʱ�ٶȴ�СΪv����x��������ļн�Ϊ����
�� L=$\frac{1}{2}g{t}_{1}^{2}$��2L=v0t1�����t1=$\sqrt{\frac{2L}{g}}$��v0=$\sqrt{2gL}$
�͵ε���N��ʱ��ֱ���ٶ� vy=gt1=$\sqrt{2gL}$
�� v=$\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}$=2$\sqrt{gL}$
�ɼ���֪ʶ��֪ tan��=$\frac{{v}_{y}}{{v}_{0}}$=1����=45��
��3����������Բ���˶��ĶԳ��Կ�֪���͵ε���P��ʱ�ٶȷ�����x��������ļн�Ϊ45�㣬��б�����Ϸ�����P��M��������糡��ƽ�⣬�͵�������ֱ���˶���
�����͵ε��˶��켣��ͼ�����͵�Բ���˶��Ĺ���뾶Ϊr���ɼ���֪ʶ�ɵ�
OP=OM=L��$\sqrt{2}$r=3L��r=$\frac{3\sqrt{2}}{2}$L
��qvB=m$\frac{{v}^{2}}{r}$�� B=$\frac{2m}{3q}\sqrt{\frac{2g}{L}}$
�����ֶ���֪�ų��ķ���ֱֽ�����⣮
��4���͵δ�N��P��ʱ�� t2=$\frac{3}{4}$T��T=$\frac{2��m}{qB}$
�ɵ� t2=$\frac{9��}{8}\sqrt{\frac{2L}{g}}$
��P��M��ʱ�� t3=$\frac{\sqrt{2}L}{v}$=$\sqrt{\frac{L}{2g}}$
����ʱ��Ϊ t=t1+t2+t3=$\sqrt{\frac{2L}{g}}$+$\frac{9��}{8}\sqrt{\frac{2L}{g}}$+$\sqrt{\frac{L}{2g}}$=$\frac{9��+12}{8}\sqrt{\frac{2L}{g}}$
��
��1���糡ǿ��E�Ĵ�С��$\frac{mg}{q}$����������ֱ���ϣ�
��2���͵ε���N��ʱ�ٶȴ�С��2$\sqrt{gL}$����x��������ļн�Ϊ45�㣻
��3����ǿ�ų��ĴŸ�Ӧǿ�ȵĴ�С��$\frac{2m}{3q}\sqrt{\frac{2g}{L}}$������ֱֽ�����⣻
��4���͵δ�M���������N��P������ֻص�M�����õ�ʱ����$\frac{9��+12}{8}\sqrt{\frac{2L}{g}}$��
���� ��Ϥƽ���˶��Ĵ�����ʽ����ƽ���˶��ֽ�����ֱ���������ֱ���˶��ͳ��ٶ�Ϊ0���ȼ���ֱ���˶���ͨ�����˶��Ĵ����õ����˶������ʣ������켣�����ü���֪ʶ����ų����˶��İ뾶���������ʱ�䣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ֱ���ɻ�����ת�������� | |
| B�� | �о��ӱ����������˶��������г� | |
| C�� | �о��г�����100��ɽ������Ҫ��ʱ�� | |
| D�� | �о��������ת |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ��һС���ڹ⻬��V�β�����A���ͷţ���B�㣨��B����ײ����ʱ�䲻�ƣ�������A��ȸߵ�C�㣬��A��ĸ߶�Ϊ1m����ȫ������С��ͨ����·�̺�λ�ƴ�С�ֱ�Ϊ��������
��ͼ��ʾ��һС���ڹ⻬��V�β�����A���ͷţ���B�㣨��B����ײ����ʱ�䲻�ƣ�������A��ȸߵ�C�㣬��A��ĸ߶�Ϊ1m����ȫ������С��ͨ����·�̺�λ�ƴ�С�ֱ�Ϊ��������| A�� | $\frac{2}{3}$$\sqrt{3}$ m��$\frac{2}{3}$$\sqrt{3}$ m | B�� | $\frac{2}{3}$$\sqrt{3}$ m��$\frac{4}{3}$$\sqrt{3}$ m | C�� | $\frac{4}{3}$$\sqrt{3}$ m��$\frac{2}{3}$$\sqrt{3}$ m | D�� | $\frac{4}{3}$$\sqrt{3}$ m��1 m |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ��С������Ϊ2Kg���ò����쳤�ij���Ϊl=0.4m����������O�㣬
��ͼ��ʾ��С������Ϊ2Kg���ò����쳤�ij���Ϊl=0.4m����������O�㣬�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | �ٶ� | B�� | ���ٶ� | C�� | ·�� | D�� | λ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ������ֵ��ͬ�Ķ�ֵ����RA=RB=RC=4�����ֽ������贮������һ��Դ���ˣ���һ���������������RA��RB���ˣ�������������RB��RC���ˣ���ͼ��ʾ����֪��Դ�ĵ綯��ΪE=4V������r=1�����������ĵ���ΪC=4��F�����رպϺ���·�ȶ�ʱ����
������ֵ��ͬ�Ķ�ֵ����RA=RB=RC=4�����ֽ������贮������һ��Դ���ˣ���һ���������������RA��RB���ˣ�������������RB��RC���ˣ���ͼ��ʾ����֪��Դ�ĵ綯��ΪE=4V������r=1�����������ĵ���ΪC=4��F�����رպϺ���·�ȶ�ʱ�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 2011��7��2������1��룬���ݱ���������������һ������Ůͯ�椲�����10¥�䣬���Ƽ�ܲ������س��ȥ����۽�ס���ӣ�ʹ������Σ�գ������˵������������Ƽȴ�ֱ۹��ۣ����˽��أ��������dz�Ϊ���������衱�������Ǵ����h2=28.5m�ߵ���̨�£���������п�������Ϊ����������0.4�����ڷ����椿�ʼ��ʱ�����Ƽ���̳���¥�£��ſ�˫���ھ����߶�h1=1.5m������۽�ס�椱���Ҿ緢����g=10m/s2������
2011��7��2������1��룬���ݱ���������������һ������Ůͯ�椲�����10¥�䣬���Ƽ�ܲ������س��ȥ����۽�ס���ӣ�ʹ������Σ�գ������˵������������Ƽȴ�ֱ۹��ۣ����˽��أ��������dz�Ϊ���������衱�������Ǵ����h2=28.5m�ߵ���̨�£���������п�������Ϊ����������0.4�����ڷ����椿�ʼ��ʱ�����Ƽ���̳���¥�£��ſ�˫���ھ����߶�h1=1.5m������۽�ס�椱���Ҿ緢����g=10m/s2�������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ������Ծij����ʱ���ٶ�Ϊ80m/s | |
| B�� | ���ɱ����������36km/h���ٶ���ʻʱΪ���� | |
| C�� | Զ���ڵ�����ڿ�ʱ���ٶ�Ϊ2 000m/s | |
| D�� | �����ٶȼ�ָʾ���ٶ�80km/h |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
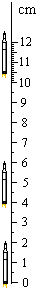 2004��7��25�գ��й��ó������ػ���ɹ��ķ����ˡ�̽����š����ǣ�ͼ��ij���ϵͳÿ��2.5s����ģ����ڼ��ٽλ����һ����Ƭ����֪����ij���Ϊ40m���ÿ̶ȳ߲�����Ƭ�ϵij��ȣ������ͼ��ʾ�������ļ��ٶ�a=8m/s2���������Ƭ�еڶ���λ������Ӧʱ�̵��ٶȴ�СΪv=42m/s��
2004��7��25�գ��й��ó������ػ���ɹ��ķ����ˡ�̽����š����ǣ�ͼ��ij���ϵͳÿ��2.5s����ģ����ڼ��ٽλ����һ����Ƭ����֪����ij���Ϊ40m���ÿ̶ȳ߲�����Ƭ�ϵij��ȣ������ͼ��ʾ�������ļ��ٶ�a=8m/s2���������Ƭ�еڶ���λ������Ӧʱ�̵��ٶȴ�СΪv=42m/s���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com