
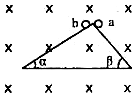
 �㹻���Ĺ⻬��Ե�ۣ���ˮƽ����ļнǷֱ�Ϊ���ͦ£������£�����ͼ��ʾ���Ӵ�ֱ��ֽ������Ĵų����ֱ�������ȣ���������������ɵ�С��a��b�����δ���б��Ķ����ɾ�ֹ�ͷţ����������ڲ��ϵ��˶�������˵���в���ȷ���ǣ�������
�㹻���Ĺ⻬��Ե�ۣ���ˮƽ����ļнǷֱ�Ϊ���ͦ£������£�����ͼ��ʾ���Ӵ�ֱ��ֽ������Ĵų����ֱ�������ȣ���������������ɵ�С��a��b�����δ���б��Ķ����ɾ�ֹ�ͷţ����������ڲ��ϵ��˶�������˵���в���ȷ���ǣ�������| A�� | �ڲ���a��b�������ȼ���ֱ���˶���aa��ab | |
| B�� | �ڲ���a��b�����������ֱ���˶���������aa��ab | |
| C�� | a��b�����ز��˶���ʱ��ֱ�Ϊta��t b��ta��tb | |
| D�� | a��b������б���˶��������ֱ�߶ȷֱ�Ϊha��hb����ha��hb |
���� ������ֱ��������������ȷ������������ţ�ٵڶ����ɿ���������ٶȣ�Ȼ��Ƚϼ��ٶȴ�С���ж�С����˶����ʣ����С����б�����˶���λ�����˶�ʱ�䣬Ȼ����⣮
��� �⣺A����С���ܵ���������������б�洹ֱ���ϣ���б�淽��ĺ���Ϊ�����ķ�����������ٶ�Ϊaa=gsin�� ab=gsin��
�ɼ�aa��ab ��A��ȷ��B����ȷ��
C�������ٵ����������������ش�ֱб�����·������ʱ��С������б��
�� mgcos��=Bqv
���ԣ�${v}_{a}=\frac{mgcos��}{qB}$��${v}_{b}=\frac{mgcos��}{qB}$
���ڣ������£�����va��vb��
����v=gsin��ta ��${t}_{a}=\frac{m}{Bqtan��}$
ͬ���� ${t}_{b}=\frac{m}{Btan��}$
��ta��tb����C��ȷ��
D���� ${v}_{a}^{2}$=2gsin��•sa ��� ${s}_{a}=\frac{g{m}^{2}��1-si{n}_{��}^{2}��}{2{B}^{2}{q}^{2}sin��}$
ͬ���ã�${s}_{b}=\frac{g{m}^{2}��1-si{n}_{��}^{2}��}{2{B}^{2}{q}^{2}sin��}$
������£��� sa��sb
����б���˶��������ֱ�߶ȣ�hma=sa•sin������hmb=sb•sin��
������֪��ha��hb����D��ȷ��
����ѡ����ȷ�ģ���ѡ��B
���� ���⿼��С����������֧�������������������µ��˶������ж����������ķ�����ȷ���С�ľ������أ�


 ������ʱ����ҵ����ϵ�д�
������ʱ����ҵ����ϵ�д� ��ĩ���ƾ�ϵ�д�
��ĩ���ƾ�ϵ�д� ���ɿ��ñ���ϵ�д�
���ɿ��ñ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
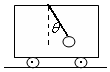 ��ͼ��ʾ������ˮƽֱ����ȱ����˶��Ļ����ᶥ��������ϵ��һС����������ƫ����ֱ����ļн�Ϊ�ȣ��ļ��ٶ��ǣ�������
��ͼ��ʾ������ˮƽֱ����ȱ����˶��Ļ����ᶥ��������ϵ��һС����������ƫ����ֱ����ļн�Ϊ�ȣ��ļ��ٶ��ǣ�������| A�� | gsin�� | B�� | gtan�� | C�� | gcos�� | D�� | gcot�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ��ʻ�����еij˿ͣ�������������ϵ���ľ����˶������Ե���Ϊ�ο�ϵ | |
| B�� | ȡ����Ϊ�������ض�������������ϵ�������x1=2m�˶���x2=-3m���ݴ˿��жϳ��������������˶���5m | |
| C�� | �ڡ�һ�ڿε�ʱ��40���ӡ��͡�У�˶����а�������ʱ����յ���ٶ�Ϊ9.2m/s�����仰�еġ�ʱ�䡱�͡��ٶȡ�����Ӧ����һ������ | |
| D�� | ������м��ٶȣ����ٶȾ�һ���ᷢ���仯 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
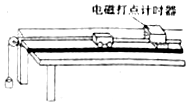 �ڡ���֤ţ�ٵڶ����ɡ���ʵ���У�С��P����ľ�����ϣ�ƽ���Ħ�����Ժ���ϸ�߿���������ƵĹ⻬����������һ������G=8N������Q��С��P�����˶��ļ��ٶ�Ϊa1����ϸ���¶˲����������F=8N������ֱ������ϸ���¶ˣ���ʱС��P�ļ��ٶ�Ϊa2��������
�ڡ���֤ţ�ٵڶ����ɡ���ʵ���У�С��P����ľ�����ϣ�ƽ���Ħ�����Ժ���ϸ�߿���������ƵĹ⻬����������һ������G=8N������Q��С��P�����˶��ļ��ٶ�Ϊa1����ϸ���¶˲����������F=8N������ֱ������ϸ���¶ˣ���ʱС��P�ļ��ٶ�Ϊa2��������| A�� | a1��a2 | B�� | a1=a2 | ||
| C�� | a1��a2 | D�� | �������㣬���ж� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ��AB���������Ƶ���M������Բ���˶�������A�Ĺ���뾶��������B�Ĺ���뾶��������A��B�����ٶȷֱ�ΪvA��vB�����ٶȷֱ�Ϊ��A����B��������
��ͼ��ʾ��AB���������Ƶ���M������Բ���˶�������A�Ĺ���뾶��������B�Ĺ���뾶��������A��B�����ٶȷֱ�ΪvA��vB�����ٶȷֱ�Ϊ��A����B��������| A�� | vA��vB����A����B | B�� | vA��vB����A����B | C�� | vA��vB����A����B | D�� | vA��vB����A����B |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ���ǵ�����Ϊ$M=\frac{{4{��^2}r_1^3}}{GT_1^2}$ | |
| B�� | ���DZ�����������ٶ�Ϊ$g'=\frac{{4{��^2}{r_1}}}{T_1^2}$ | |
| C�� | ��½����r1��r2������˶�ʱ���ٶȴ�С֮��Ϊ$\frac{v_1}{v_2}=\sqrt{\frac{{{m_1}{r_2}}}{{{m_2}{r_1}}}}$ | |
| D�� | ��½���ڰ뾶Ϊr2�������Բ���˶�������Ϊ${T_2}=\frac{{r_2^{\;}}}{{r_1^{\;}}}{T_1}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
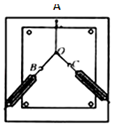 ����֤����ƽ���ı��ζ���ʵ�������ͼ��ʾ������AΪ�̶���Ƥ���ͼ����OΪ��Ƥ����ϸ���Ľ�㣬OB��OCΪϸ����
����֤����ƽ���ı��ζ���ʵ�������ͼ��ʾ������AΪ�̶���Ƥ���ͼ����OΪ��Ƥ����ϸ���Ľ�㣬OB��OCΪϸ�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ��ʾ������ǿ�ų��У�һ������Ȧ�ƴ�ֱ�Ÿ��ߵĶԳ���OO���Խ��ٶȦ�����ת������Ȧ����Ϊr������ΪN�����ΪS����ͼʾλ��ת��90��Ĺ����У�����˵����ȷ���ǣ�������
��ͼ��ʾ������ǿ�ų��У�һ������Ȧ�ƴ�ֱ�Ÿ��ߵĶԳ���OO���Խ��ٶȦ�����ת������Ȧ����Ϊr������ΪN�����ΪS����ͼʾλ��ת��90��Ĺ����У�����˵����ȷ���ǣ�������| A�� | ͨ������R�ĵ����Ϊq=$\frac{NBS}{R+r}$ | |
| B�� | ͨ������R�ĵ����Ϊq=$\frac{��NBS}{2\sqrt{2}��R+r��}$ | |
| C�� | ����������ƽ������ΪP=$\frac{{N}^{2}{B}^{2}{S}^{2}{��}^{2}}{2��R+r��}$ | |
| D�� | ����������ƽ������ΪP=$\frac{{N}^{2}{B}^{2}{S}^{2}{��}^{2}R}{2��R+r��^{2}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����

| U/V | 0 | 0.40 | 0.60 | 0.80 | 1.00 | 1.20 | 1.32 | 1.50 |
| I/A | 0 | 0.20 | 0.45 | 0.80 | 1.25 | 1.80 | 2.20 | 2.81 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com