
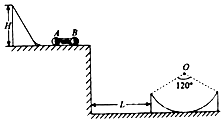
 如图所示,小球A和B质量为mA=0.3kg和mB=0.5kg,两球间压缩一弹簧(不栓接),并用细线连接,静止于一光滑的平台上,烧断细线后A球滑上用一小段圆弧连接的光滑斜面,当滑到斜面顶端时速度刚好为零,斜面的高度H=1.25m,B球滑出平台后刚好沿右侧光滑圆槽顶端的切线方向进入槽中,圆形槽的半径R=3m,圆形槽所对的圆心角为120°,g=10m/s2,求:
如图所示,小球A和B质量为mA=0.3kg和mB=0.5kg,两球间压缩一弹簧(不栓接),并用细线连接,静止于一光滑的平台上,烧断细线后A球滑上用一小段圆弧连接的光滑斜面,当滑到斜面顶端时速度刚好为零,斜面的高度H=1.25m,B球滑出平台后刚好沿右侧光滑圆槽顶端的切线方向进入槽中,圆形槽的半径R=3m,圆形槽所对的圆心角为120°,g=10m/s2,求:分析 (1)对A应用机械能守恒求解;
(2)由动量守恒求得B做平抛运动的初速度,然后根据末速度方向求得竖直分速度,进而得到运动时间,从而求得距离;
(3)对B球在圆形槽上的运动应用机械能守恒求得在最低点的速度,然后由牛顿第二定律求得支持力,即可由牛顿第三定律求得压力.
解答 解:(1)烧断细线后,A球到达斜面顶端的过程只有重力做功,机械能守恒,故有:$\frac{1}{2}{m_A}v_A^2={m_A}gH$
解得:${v}_{A}=\sqrt{2gH}=5m/s$;
(2)A、B球在烧断绳子的过程动量守恒,故有:mAvA=mBvB
解得:${v}_{B}=\frac{{m}_{A}}{{m}_{B}}{v}_{A}=3m/s$;
B球滑出平台后做平抛运动,刚好沿光滑固定圆槽左边顶端的切线方问进入槽中,
根据几何关系得:$tan60°=\frac{v_y}{v_B}$
解得:${v}_{y}={v}_{B}tan60°=3\sqrt{3}m/s$;
则小球做平抛运动的时间为:$t=\frac{v_y}{g}$=$\frac{3\sqrt{3}}{10}s$;
水平方向做匀速运动,则有平台到圆形槽的距离为:$L={v}_{B}t=\frac{9\sqrt{3}}{10}m=1.56m$;
(3)对小球从圆槽最高点到圆槽最低点的过程只有重力做功,机械能守恒,
小球在最高点速度为:$v=\sqrt{v_B^2+v_y^2}=2{v_B}=6m/s$;
小球从圆槽的最高抵到最低点距离为:$h=R(1-cos60°)=\frac{1}{2}R=\frac{3}{2}m$;
再设小球在最低点速度为v1,根据机械能守恒有:$\frac{1}{2}{m}_{B}{{v}_{1}}^{2}={m}_{B}gh+\frac{1}{2}{m}_{B}{v}^{2}$;
在最低点,根据牛顿第二定律得:${F_N}-{m}_{B}g={m}_{B}\frac{v_1^2}{R}$;
解得:${F}_{N}={m}_{B}g+\frac{{m}_{B}{{v}_{1}}^{2}}{R}={m}_{B}g+\frac{2{m}_{B}gh+{m}_{B}{v}^{2}}{R}$=16N;
根据牛顿第三定律可知,小球B滑到圆槽最低点时对糟的压力为16N,方向竖直向下;
答:(1)烧断细线后,小球A脱离弹簧时的速度vA为5m/s;
(2)平台到圆形槽的距离为1.56m;
(3)小球B滑到圆形槽最低点时对槽的压力为16N,方向竖直向下.
点评 经典力学问题一般先对物体进行受力分析,求得合外力及运动过程做功情况,然后根据牛顿定律、动能定理及几何关系求解.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中物理 来源: 题型:计算题
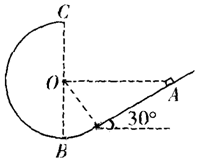 如图所示,竖直平面内一半径为R的光滑圆弧形内轨道与倾角θ=30°的粗糙斜面连接,连接处与光滑圆弧相切,质量为m,可视为质点的物块从斜面上与圆心等高的A点以初速度v0滑下,经过圆心正上方的轨道最高点C抛出后,恰又落到A点.设物块与斜面间动摩擦因数μ=0.2,重力加速度为g,求:
如图所示,竖直平面内一半径为R的光滑圆弧形内轨道与倾角θ=30°的粗糙斜面连接,连接处与光滑圆弧相切,质量为m,可视为质点的物块从斜面上与圆心等高的A点以初速度v0滑下,经过圆心正上方的轨道最高点C抛出后,恰又落到A点.设物块与斜面间动摩擦因数μ=0.2,重力加速度为g,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
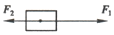 如图所示,物块受到F1、F2两个水平拉力作用.已知F1和F2分别为5N 和3N,那么这两个拉力的合力为( )
如图所示,物块受到F1、F2两个水平拉力作用.已知F1和F2分别为5N 和3N,那么这两个拉力的合力为( )| A. | 2N | B. | 3N | C. | 5N | D. | 8N |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 磁感线上各点的切线方向就是各点的磁感应强度的方向 | |
| B. | 磁感线是磁场中客观存在的曲线 | |
| C. | 铁屑在磁场中分布所形成的曲线就是磁感线 | |
| D. | 磁感线总是从磁体N极出发指向磁体的S极 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题

查看答案和解析>>
科目:高中物理 来源: 题型:计算题
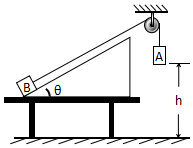 如图所示,倾角θ=37°的斜面体固定在水平桌面上,质量M=2.0kg的物体B放在斜面底端,与斜面间的动摩擦因数μ=0.25,现通过轻细绳跨过光滑的定滑轮与质量m=2.5kg的A物体相连接,连接B的细绳与斜面平行.若用手托住A物体,使其在距地面h=2m高处由静止释放,A物体着地后立即停止运动,A、B物体均可视为质点,取g=10m/s2,sin37°=0.6,cos37°=0.8.求:
如图所示,倾角θ=37°的斜面体固定在水平桌面上,质量M=2.0kg的物体B放在斜面底端,与斜面间的动摩擦因数μ=0.25,现通过轻细绳跨过光滑的定滑轮与质量m=2.5kg的A物体相连接,连接B的细绳与斜面平行.若用手托住A物体,使其在距地面h=2m高处由静止释放,A物体着地后立即停止运动,A、B物体均可视为质点,取g=10m/s2,sin37°=0.6,cos37°=0.8.求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,在斯特林循环的P-V图象中,一定质量理想气体从状态a依次经过状态b、c和d后再回到状态a,整个过程由两个等温和两个等容过程组成.下列说法正确的是( )
如图所示,在斯特林循环的P-V图象中,一定质量理想气体从状态a依次经过状态b、c和d后再回到状态a,整个过程由两个等温和两个等容过程组成.下列说法正确的是( )| A. | 从a到b,气体得温度一直升高 | |
| B. | 从b到c,气体与外界无热量交换 | |
| C. | 从c到d,气体对外放热 | |
| D. | 从d到a,单位体积中的气体分子数目增大 | |
| E. | 从b到c气体吸收得热量与从d到a气体气体放出得热量相同 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 速度大的绳的拉力大 | B. | 所需时间相同 | ||
| C. | 功率一样大 | D. | 做的功一样多 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
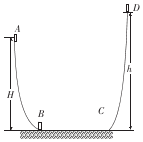 如图所示,ABCD为一竖直平面的轨道,其中BC水平,A点比BC高出10m,BC长为2m,AB和CD轨道光滑,且均与BC平滑连接.一质量为0.5kg的物体,从A点以6m/s的速度开始运动,经过BC后滑到高出 C点10.8m的D点时其速度为零,已知物体第一次从A点运动到B点的过程中,所用时间为0.8s,取g=10m/s2.求:
如图所示,ABCD为一竖直平面的轨道,其中BC水平,A点比BC高出10m,BC长为2m,AB和CD轨道光滑,且均与BC平滑连接.一质量为0.5kg的物体,从A点以6m/s的速度开始运动,经过BC后滑到高出 C点10.8m的D点时其速度为零,已知物体第一次从A点运动到B点的过程中,所用时间为0.8s,取g=10m/s2.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com