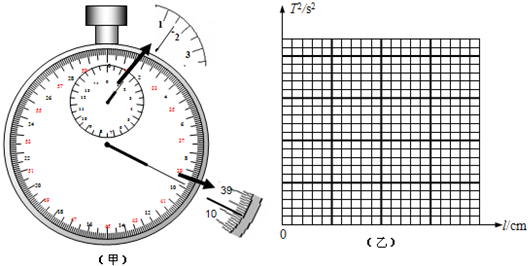
解:(1)①设0到A之间的距离叫x
1,设A到B之间的距离叫x
2,设B到C之间的距离叫x
3,设C到D之间的距离叫x
4,设D到E之间的距离叫x
5,设E到F之间的距离叫x
6,
根据匀变速直线运动的推论公式△x=aT
2可以求出加速度的大小,
得:x
4-x
1=3a
1T
2 x
5-x
2=3a
2T
2 x
6-x
3=3a
3T
2 为了更加准确的求解加速度,我们对三个加速度取平均值
得:a=

(a
1+a
2+a
3)
代入数据解得a=2.05m/s
2.
②因为每两点之间还有四点没有画出来,所以T=0.1s,根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,
v
D=
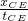
=1.22m/s
(2)①设楼高h,设第一个小球下落时间为t,第二个小球落地时间t+△t,
对第一个落地小球列一个位移时间关系:h=

gt
2 ①
对第二个落地小球列一个位移时间关系:h+L=

g(t+△t)
2②
①②两式中含有h和t两个未知数,所以从原理上讲这个方案正确.
②从实际测量来看,最大的困难是△t太小,难以测量.
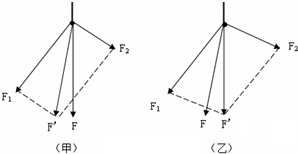
(3)方案(a),通过弹簧测力计的示数来得到摩擦力的大小,木块只有在匀速运动的过程中,才能使用利用二力平衡条件,根据F=μG得:
μ=
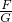
;所以要测量弹簧秤示数F和木块的重量G;
方案(b):无论长木板是否做匀速直线运动,木块都相对于木板滑动且始终处于平衡状态,这样拉力等于摩擦力,而且无论拉木板速度多少,摩擦力都一样,不改变摩擦力大小,所以容易操作;所以方案b更合理;要测量弹簧秤示数F和木块的重量G;
故答案为:
(1)a=2.05 v=1.22
(2)①可行 理由:h=

gt
2,h+L=

g(t+△t)
2,两个方程,两个未知数,方程可解,
②最大困难:△t的测量
(3)b,弹簧秤示数F和木块的重量G
分析:1、根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上D点时小车的瞬时速度大小,根据匀变速直线运动的推论公式△x=aT
2可以求出加速度的大小.
2、可设第一个小球下落时间为t,由自由落体的位移时间公式可表示出下落的位移,即楼的高度;在对第二个落地小球列一个位移时间关系式.
3、第一种方案要匀速,利用二力平衡条件求得μ,但是匀速运动难控制;第二种方案木块保持静止,一定平衡;根据平衡条件列式后确定待测量.
点评:1、要提高应用匀变速直线的规律以及推论解答实验问题的能力,在平时练习中要加强基础知识的理解与应用.
要注意单位的换算和有效数字的保留.
2、解决自由落体运动的题目关键在于明确自由落体中的公式应用,一般情况下,研究由落点开始的运动列出的表达式最为简单;并且最好尝试一题多解的方法.
3、本题是探究性实验,关键明确实验原理,要尽量减小实验误差,难度不大,属于基础题.


 (a1+a2+a3)
(a1+a2+a3)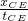 =1.22m/s
=1.22m/s gt2 ①
gt2 ① g(t+△t)2②
g(t+△t)2②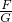 ;所以要测量弹簧秤示数F和木块的重量G;
;所以要测量弹簧秤示数F和木块的重量G; gt2,h+L=
gt2,h+L= g(t+△t)2,两个方程,两个未知数,方程可解,
g(t+△t)2,两个方程,两个未知数,方程可解,

 (1)某同学在做多用电表测电阻的实验中:测量某电阻时,用“×10Ω”档时发现指针偏转角度过大,他应该换用
(1)某同学在做多用电表测电阻的实验中:测量某电阻时,用“×10Ω”档时发现指针偏转角度过大,他应该换用