
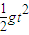 ,那么就可以求出小球开始做平抛运动的位置坐标
,那么就可以求出小球开始做平抛运动的位置坐标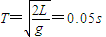
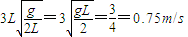
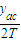 =
=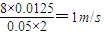
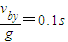
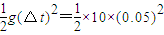 m=1.25cm
m=1.25cm

 优等生题库系列答案
优等生题库系列答案科目:高中物理 来源: 题型:
 下列关于几个实验的说法正确的是
下列关于几个实验的说法正确的是查看答案和解析>>
科目:高中物理 来源: 题型:
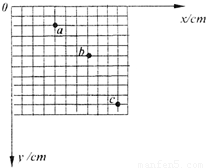
 在“研究平抛运动”的实验中,记录的点迹如图所示,图中每个方格边长L=2.5cm,g=10m/s2,若小球在平抛途中的几个位置如图中的a、b、c、d各点所示,则小球的初速度的计算表达式为v0=
在“研究平抛运动”的实验中,记录的点迹如图所示,图中每个方格边长L=2.5cm,g=10m/s2,若小球在平抛途中的几个位置如图中的a、b、c、d各点所示,则小球的初速度的计算表达式为v0=| gL |
| gL |
查看答案和解析>>
科目:高中物理 来源: 题型:
 在研究平抛运动的实验中,小球必须每次从斜槽上的同一位置落下,是为了使小球离开斜槽末端的
在研究平抛运动的实验中,小球必须每次从斜槽上的同一位置落下,是为了使小球离开斜槽末端的
|
|
| gL |
| gL |
查看答案和解析>>
科目:高中物理 来源: 题型:
 (1)在研究平抛运动的实验中,让小球多次从斜槽上滚下,在白纸上依次记下小球的位置,某甲和某乙得到的记录纸分别如图所示,从图中明显看出甲的实验错误是
(1)在研究平抛运动的实验中,让小球多次从斜槽上滚下,在白纸上依次记下小球的位置,某甲和某乙得到的记录纸分别如图所示,从图中明显看出甲的实验错误是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com