儿童练习游泳时穿的一种“救生衣”实质是将泡沫塑料包在背心上,使用时,穿上这种“救生衣”泡沫塑料位于人的胸部,为了确保儿童的安全,必须使人的头部露出水面,儿童体重约300牛,人的密度约为1.06×103kg/m3,人的头部约占人体总体积的十分之一,泡沫塑料的密度约为10kg/m3,求:
( 1 )此儿童的体积大约是多少?
( 2 )此儿童仅头部露出水面时受到多大的浮力?
( 3 )此儿童使用的“救生衣”的最小体积为多大才能保证儿童的安全?
解:(1)根据密度定义式
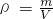
和G=mg,得到
G
人=m
人g=ρ
人V
人g
故V
人=

即此儿童的体积大约是2.89×10
-2m
3.
(2)人浸入水中的体积为
V
排=V
人-

V
人=
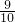
V
人=0.9×2.89×10
-2m
3=2.6×10
-2m
3F
浮=

即此儿童仅头部露出水面时受到20N的浮力.
(3)F
浮’=G
总F
浮+ρ
水gV=G
人gV
V=

≈4×10
-3m
3即此儿童使用的“救生衣”的最小体积为4×10
-3m
3才能保证儿童的安全.
分析:(1)根据密度定义式
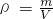
和G=mg直接求解儿童的体积;
(2)根据题意先计算出人排开水的体积,然后根据阿基米德定律求解受到的浮力;
(3)假设“救生衣”恰好使儿童头部浮出水面,对“救生衣”和人整体受力分析,根据平衡条件列式求解即可.
点评:本题关键通过阿基米德定律求出水的浮力,人和救生衣整体受力平衡,根据二力平衡列方程求解.

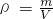 和G=mg,得到
和G=mg,得到
 V人=
V人=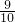 V人=0.9×2.89×10-2m3=2.6×10-2m3
V人=0.9×2.89×10-2m3=2.6×10-2m3
 ≈4×10-3m3
≈4×10-3m3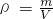 和G=mg直接求解儿童的体积;
和G=mg直接求解儿童的体积;

 阅读快车系列答案
阅读快车系列答案