
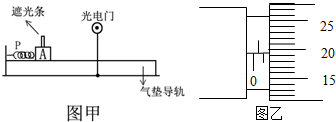
分析 (2)螺旋测微器读数方法为固定部分刻度加上转动部分刻度与0.01的乘积;
(3)经过光电门的平均速度等于该点的瞬时速度,由平均速度公式求解;
(4)由动能公式求解动能,再由能量守恒可求得弹簧的弹性势能;
(5)由弹簧弹性势能的表达式可求得劲度系数.
解答 解:(2)由螺旋测微器的读数方法可知,读数为:1.0mm+19.5×0.01=1.195mm;
(3)经过光电门的平均速度可视为该点的瞬时速度,则有:v=$\frac{d}{t}$;
(4)物体获得的动能EK=$\frac{1}{2}$mv2=$\frac{1}{2}$×0.1×($\frac{0.001195}{1.195×1{0}^{-4}}$)2=5J;由能量守恒可知,弹簧的弹性势能等于物体的动能,即EP=5J;
(5)由能量守恒可知,弹簧的弹性势能等于物体的动能,故5=$\frac{1}{2}$kx2;
解得:
K=4000N/m;
故答案为:(2)1.195; (3)$\frac{d}{t}$; (4)5J; (5)4000N/m
点评 本题考查了螺旋测微器的读数原理、胡克定理及能量守恒定律的应用,要注意明确实验原理,能通过分析得出弹性势能的计算方法.


科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 密闭在容器中的气体,在某一时刻向各个方向运动的气体分子数目一定相等 | |
| B. | 大量气体分子的速率有大有小,但是按“中间多,两头少”的规律分布 | |
| C. | 气体压强的大小跟气体分子的平均动能、分子的密集程度这两个因素有关 | |
| D. | 一定质量的理想气体,温度不变,体积减小时,气体的内能一定增大 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 向心加速度大小与轨道半径成正比 | B. | 向心加速度大小与轨道半径成反比 | ||
| C. | 向心加速度方向与向心力方向一致 | D. | 向心加速度指向圆心 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,光滑的水平地面上有一辆平板车,车上有一个人.原来车和人都静止.当人从左向右行走的过程中( )
如图所示,光滑的水平地面上有一辆平板车,车上有一个人.原来车和人都静止.当人从左向右行走的过程中( )| A. | 人和车组成的系统水平方向动量不守恒 | |
| B. | 人和车组成的系统机械能守恒 | |
| C. | 人和车的速度方向相同 | |
| D. | 人停止行走时,人和车的速度一定均为零 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,验电器带有少量正电荷,将一带负电的小球从远处逐渐靠近验电器的金属球,此过程可能看到金属箔片张开的角度( )
如图所示,验电器带有少量正电荷,将一带负电的小球从远处逐渐靠近验电器的金属球,此过程可能看到金属箔片张开的角度( )| A. | 不断增大 | B. | 先减小至零,后逐渐增大 | ||
| C. | 先增大,后减小 | D. | 先增大,后不变 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | α粒子散射实验现象 | B. | 慢中子轰击铀核产生的裂变现象 | ||
| C. | 天然放射现象中的α衰变现象 | D. | 氢原子光谱的特征谱线现象 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 1×104N | B. | 1×103N | C. | 7.35×104N | D. | 7.35×103N |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
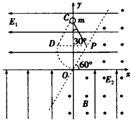 如图所示,在xOy竖直平面内,长L的绝缘轻绳一端固定在第一象限的P点,另一端栓有一质量为m、带电荷量为+q的小球,OP距离也为L且与x轴的夹角为60°.在x轴上方有水平向左的匀强电场,场强大小为$\frac{\sqrt{3}mg}{3q}$,在x轴下方有竖直向上的匀强电场,场强大小为$\frac{mg}{q}$,过O和P两点的虚线右侧存在方向垂直xOy平面向外、磁感应强度为B的匀强磁场.小球置于y轴上的C点时,绳恰好伸直且与y轴夹角为30°,小球由静止释放后将沿CD方向做直线运动,到达D点时绳恰好绷紧,小球沿绳方向的分速度立即变为零,并以垂直于绳方向的分速度摆下,到达O点时将绳断开.不计空气阻力.求:
如图所示,在xOy竖直平面内,长L的绝缘轻绳一端固定在第一象限的P点,另一端栓有一质量为m、带电荷量为+q的小球,OP距离也为L且与x轴的夹角为60°.在x轴上方有水平向左的匀强电场,场强大小为$\frac{\sqrt{3}mg}{3q}$,在x轴下方有竖直向上的匀强电场,场强大小为$\frac{mg}{q}$,过O和P两点的虚线右侧存在方向垂直xOy平面向外、磁感应强度为B的匀强磁场.小球置于y轴上的C点时,绳恰好伸直且与y轴夹角为30°,小球由静止释放后将沿CD方向做直线运动,到达D点时绳恰好绷紧,小球沿绳方向的分速度立即变为零,并以垂直于绳方向的分速度摆下,到达O点时将绳断开.不计空气阻力.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com