

分析 (1)由动能定理即可求出粒子的速度,由位移公式即可求出长度l;
(2)由半径公式即可求出磁感应强度,由位移公式即可求出时间;
(3)通过运动的轨迹与速度的方向分析能否发生碰撞.
解答 解:(1)质子加速的过程中,电场力做功,得:$e{U}_{0}=\frac{1}{2}m{v}^{2}-\frac{1}{2}m{v}_{0}^{2}$
将eU0=$\frac{3}{2}$mv02代入得:v=2v0
由于是相同的粒子,又在相同的电场中加速,所以可知,所有粒子在电场中加速的时间是相等的,在加速 之前,进入电场的时间差:$t=\frac{{l}_{0}}{{v}_{0}}$
出电场的时间差也是△t,所以,出电场后,该质子束的长度:L=vt=2v0t=2l0
(2)粒子在匀强磁场中做匀速圆周运动,在偏转后粒子若发生碰撞,则只有在粒子偏转90°时,才可能发生碰撞,所以碰撞的位置在OO′的连线上.
洛伦兹力提供向心力,即:$evB=\frac{m{v}^{2}}{R}$
所以:B=$\frac{mv}{eR}$=$\frac{2m{v}_{0}}{eR}$
由于洛伦兹力只改变磁场的方向,不改变粒子的速度,所以粒子经过磁场后的速度的大小不变,由于所有粒子的速度大小相等,所以应先后到达同一点,所以碰撞的时间:△t=$\frac{L}{v}=\frac{2{l}_{0}}{2{v}_{0}}=\frac{{l}_{0}}{{v}_{0}}$
(3)某次实验时将磁场O的圆心往上移了$\frac{R}{2}$,其余条件均不变,则质子束经过电场加速后的速度不变,而运动的轨迹不再对称.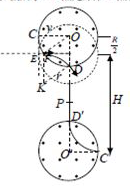
对于上边的粒子,不是对着圆心入射,而是从F点入射,如图:E点是原来C点的位置,连接OF、OD,作FK平行而且等于OD,再连接KD,由于OD=OF=FK,则四边形ODFK是菱形,即KD=KF,所以粒子仍然从D点射出,但方向不是沿OD的方向,K为粒子束的圆心.
由于磁场向上移了$\frac{1}{2}R$,故:$sin∠COF=\frac{\frac{1}{2}R}{R}=\frac{1}{2}$
得:$∠COF=\frac{π}{6}$,$∠DOF=∠FKD=\frac{π}{3}$
而对于下边的粒子,没有任何的改变,故两束粒子若相遇,则一定在D点相遇.
下方的粒子到达C′后先到达D点的粒子需要的时间:$t′=\frac{\frac{πR}{2}+(H+\frac{1}{2}R-2R)}{2{v}_{0}}=\frac{π+4}{4{v}_{0}}R$
而上方的粒子到达E点后,最后到达D点的粒子需要的时间:$t=\frac{l+\overline{EF}+\overline{FD}}{2{v}_{0}}=\frac{2{l}_{0}+(R-Rsin\frac{π}{3})+\frac{π}{3}R}{2{v}_{0}}$=$\frac{2{l}_{0}+\frac{6+2π-3\sqrt{3}}{6}R}{2{v}_{0}}$
若t′>t.即当${l}_{0}<\frac{π+3\sqrt{3}+6}{12}R$时,两束粒子不会相遇;
若t′<t.即当${l}_{0}≥\frac{π+3\sqrt{3}+6}{12}R$时,两束粒子可能相碰撞的最长时间:△t=t-t′=$\frac{{l}_{0}}{{v}_{0}}-\frac{π+3\sqrt{3}+6}{12{v}_{0}}R$
答:(1)质子束经过加速电场加速后(未进入磁场)的速度是2v0,长度是2l0;
(2)试求出磁场磁感应强度是$\frac{2m{v}_{0}}{eR}$,粒子束可能发生碰撞的时间是$\frac{{l}_{0}}{{v}_{0}}$.
(3)若某次实验时将磁场O的圆心往上移了$\frac{R}{2}$,其余条件均不变,当${l}_{0}<\frac{π+3\sqrt{3}+6}{12}R$时,两束粒子不会相遇;
当${l}_{0}≥\frac{π+3\sqrt{3}+6}{12}R$时,两束粒子可能相碰撞的最长时间:△t=t-t′=$\frac{{l}_{0}}{{v}_{0}}-\frac{π+3\sqrt{3}+6}{12{v}_{0}}R$.
点评 该题属于分析物理实验的题目,虽然给出的情况比较新颖,但是,只有抓住带电粒子在电场中运动的规律与带电粒子在磁场中运动的规律,使用动能定理与磁场中的半径公式即可正确解答.中档题目.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示一个平行板电容器水平放置,并与一金属圆环连接,一质量为m的带电小球用绝缘线悬挂在上极板上,金属环处在竖直平面内,环面与磁感应强度为B的匀强磁场垂直.若金属环、电容器及小球一起以水平速度v向右平动时,细线拉力大小为F1,且此时细线恰好处于竖直状态,若金属环、电容器及小球一起以水平速度2v向右平动时,细线拉力大小为F2,则( )
如图所示一个平行板电容器水平放置,并与一金属圆环连接,一质量为m的带电小球用绝缘线悬挂在上极板上,金属环处在竖直平面内,环面与磁感应强度为B的匀强磁场垂直.若金属环、电容器及小球一起以水平速度v向右平动时,细线拉力大小为F1,且此时细线恰好处于竖直状态,若金属环、电容器及小球一起以水平速度2v向右平动时,细线拉力大小为F2,则( )| A. | 当速度为2v时,细线与竖直方向有一向左的偏角,且F1>F2 | |
| B. | 当速度为2v时,细线仍保持竖直方向,且F1=F2 | |
| C. | 当速度为2v时,细线与竖直方向有一向右的偏角,且F1<F2 | |
| D. | 细线的拉力大小与小球所带电的电性无关 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,一个质量为m的小球用一根长为L的细线系住悬挂在天花板上,小球以角速度ω在水平面上匀速圆周运动(这种运动也叫圆锥摆),求:
如图所示,一个质量为m的小球用一根长为L的细线系住悬挂在天花板上,小球以角速度ω在水平面上匀速圆周运动(这种运动也叫圆锥摆),求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,在倾角为37°的斜坡上,从A点水平抛出一个物体,物体落在斜坡的B点,测得AB两点间的距离是75m.取g=10m/s2.(sin37°=0.6,cos37°=0.8)求:
如图所示,在倾角为37°的斜坡上,从A点水平抛出一个物体,物体落在斜坡的B点,测得AB两点间的距离是75m.取g=10m/s2.(sin37°=0.6,cos37°=0.8)求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,在一根较长的铁钉上,用漆包线绕两个线圈A和B.将线圈B的两端与漆包线CD相连,使CD平放在静止的小磁针的正上方,与小磁针平行.试判断合上开关的瞬间,小磁针N极的偏转情况?线圈A中电流稳定后,小磁针又怎样偏转?
如图所示,在一根较长的铁钉上,用漆包线绕两个线圈A和B.将线圈B的两端与漆包线CD相连,使CD平放在静止的小磁针的正上方,与小磁针平行.试判断合上开关的瞬间,小磁针N极的偏转情况?线圈A中电流稳定后,小磁针又怎样偏转?查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 任意2s内的位移一定等于1s内位移的2倍 | |
| B. | 任意一段时间内的位移大小一定等于它的路程 | |
| C. | 若两物体的速度相同,则它们的速率必然相同,在相同时间内通过的路程相等 | |
| D. | 若两物体的速率相同,则它们的速度必然相同,在相同时间内的位移相等 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,一带正电粒子质量为m,带电量为q,从隔板ab上一个小孔P处于隔板成45°角垂直于磁感线射入磁感应强度为B的单边界匀强磁场,粒子初速度大小为v,不计粒子的重力,则:
如图所示,一带正电粒子质量为m,带电量为q,从隔板ab上一个小孔P处于隔板成45°角垂直于磁感线射入磁感应强度为B的单边界匀强磁场,粒子初速度大小为v,不计粒子的重力,则:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com