
 如图所示,在矩形区域ABCD内有垂直于纸平面向里的匀强磁场,磁感应强度大小为B=5.0×10-2T,矩形区域长为0.64m,宽为0.2m,在BC边中点O处有一电粒子发射器,某时刻,发射源O沿纸面向磁场中0-180°范围垂直磁场方向均匀地辐射出速率均为v=2×l06m/s的某种带正电粒子,带电粒子质量m=2.4×10-26kg,电荷量为q=-4.8×l0-18C(不计粒子重力),求:
如图所示,在矩形区域ABCD内有垂直于纸平面向里的匀强磁场,磁感应强度大小为B=5.0×10-2T,矩形区域长为0.64m,宽为0.2m,在BC边中点O处有一电粒子发射器,某时刻,发射源O沿纸面向磁场中0-180°范围垂直磁场方向均匀地辐射出速率均为v=2×l06m/s的某种带正电粒子,带电粒子质量m=2.4×10-26kg,电荷量为q=-4.8×l0-18C(不计粒子重力),求:分析 (1)根据洛伦兹力提供向心力列方程求解;
(2)所有粒子的运动半径相同,所以弦最短的圆弧所对应的圆心角最小,运动时间最短.
(3)与BC相切的即为从CD边射出磁场的最上边缘的粒子,从D点射出的为从CD边射出的最下边缘的粒子,求出从这两点射出的粒子入射方向间的夹角,因为放射源向磁场内各方向均匀地辐射粒子,所以能从CD边射出的粒子数目为:n=$\frac{△θ}{π}$N.
解答 解:(1)洛伦兹力提供向心力:qvB=m$\frac{{v}^{2}}{R}$,解得:R=$\frac{mv}{qB}$=0.2m;
(2)因为所有粒子的轨迹半径相同,所以弦最短的圆弧所对应的圆心角最小,
运动时间最短,作EO⊥AD,EO弦最短,
因为:OE=0.2m,且R=0.2m
所以对应的圆心角为:θ=$\frac{π}{3}$,
由牛顿第二定律得:qvB=m($\frac{2π}{T}$)2R,
解得:T=$\frac{2πm}{qB}$,
最短时间为:t=$\frac{θ}{2π}$T=$\frac{θm}{qB}$=$\frac{πm}{3qB}$=$\frac{π}{3}$×10-7s;
(3)判断从O点哪些方向射入磁场的粒子将会从CD边射出,如图为两个边界,
当速度方向满足一定条件时,粒子将从C点射出磁场,OC=0.32m,且R=0.2m
由三角函数知识可知:sin$\frac{1}{2}$∠OO2C=$\frac{\frac{OC}{2}}{R}$=0.8,则∠OO2C=106°
此时射入磁场的粒子速度方向与OC夹角为53°,
当轨迹圆与BC边相切时,因为R=0.2m,CD=0.2m,可知圆心O1在BC边上,
因为OO1<OC,所以带电粒子不可能通过D点,
与AD相切的即为从CD边射出磁场的最上边缘的粒子,
该粒子进入磁场的速度方向垂直BC向上,与OC之间的夹角为90°,
所以从CD边射出的粒子,射入磁场时速度方向应与OC边夹角在53°到90°之间△θ=37°的范围内,
因为放射源向磁场内各方向均匀地辐射粒子,
所以能从CD边射出的粒子数目为:n=$\frac{△θ}{180°}$N,即:n=$\frac{37}{180}$N;
如图所示,由几何知识得:CF=$\sqrt{{R}^{2}-{O}_{1}{C}^{2}}$=$\sqrt{{R}^{2}-(OC-R)^{2}}$=$\sqrt{0.{2}^{2}-(0.32-0.2)^{2}}$=0.16m;
答:(1)带电粒子在磁场中做圆周运动的半径为0.2m;
(2)从AD边界射出的粒子中,在磁场中运动的最短时间为$\frac{π}{3}$×10-7s;
(3)若放射源向磁场内共辐射出了N个粒子,从CD边界射出的粒子有$\frac{37}{180}$N个,从CD边上粒子射出的范围是:CF=0.16m.
点评 解决题目的关键是找出临界情况,并画出临界情况下磁场中运动的轨迹,确定边界范围,找到与之对应的入射角及对应的圆心角.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中物理 来源: 题型:解答题
 如图所示,A、B两车从同一地点向同一方向运动.A做初速度为9m/s的匀减速直线运动,其加速度的大小为2m/s2;B做初速度为零的匀加速直线运动.经过3s两车速度相等,求:
如图所示,A、B两车从同一地点向同一方向运动.A做初速度为9m/s的匀减速直线运动,其加速度的大小为2m/s2;B做初速度为零的匀加速直线运动.经过3s两车速度相等,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
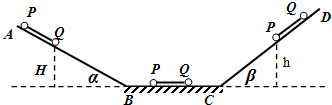
| A. | h=H | B. | h=H+Lsinβ | ||
| C. | h=H+$\frac{L(sinα-sinβ)}{5}$ | D. | h=H+$\frac{L(3sinα-2sinβ)}{5}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
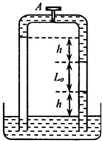 如图所示,两端开口、粗细均匀的足够长玻璃管插在大水银槽中,管的顶部有一定长度的水银.两段空气柱被封闭在左右两侧的竖直管中.开启顶部连通左右水银的阀门,右侧空气柱长为L0,右侧空气柱底部水银面比槽中水银面高出h,右侧空气柱顶部水银面比左侧空气柱顶部水银面低h.
如图所示,两端开口、粗细均匀的足够长玻璃管插在大水银槽中,管的顶部有一定长度的水银.两段空气柱被封闭在左右两侧的竖直管中.开启顶部连通左右水银的阀门,右侧空气柱长为L0,右侧空气柱底部水银面比槽中水银面高出h,右侧空气柱顶部水银面比左侧空气柱顶部水银面低h.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
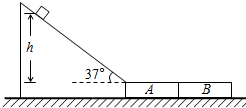 如图所示,某货场需要将质量为m=10kg的货物(可视为质点)从高处运送到地面,现利用固定在地面上的倾斜轨道传递货物,使货物由轨道顶端无初速度滑下,轨道与水平面成θ=37°角.地面上紧靠轨道依次排放两块完全相同的木板A,B,长度均为l=1.6米,厚度不计,质量为m=10kg,木板上表面与轨道末端平滑连接.货物与倾斜轨道间动摩擦因数为μ0=0.125,货物与木板间的动摩擦因数μ1,木板与地面间的动摩擦因μ2=0.2.
如图所示,某货场需要将质量为m=10kg的货物(可视为质点)从高处运送到地面,现利用固定在地面上的倾斜轨道传递货物,使货物由轨道顶端无初速度滑下,轨道与水平面成θ=37°角.地面上紧靠轨道依次排放两块完全相同的木板A,B,长度均为l=1.6米,厚度不计,质量为m=10kg,木板上表面与轨道末端平滑连接.货物与倾斜轨道间动摩擦因数为μ0=0.125,货物与木板间的动摩擦因数μ1,木板与地面间的动摩擦因μ2=0.2.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
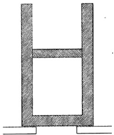 如图,导热性能良好的气缸放置在水平平台上,活塞质量m=10kg,横截面积S=50cm2,大气压强为p0=l×105Pa,当温度为t1=-3℃时,活塞封闭的气柱长L1=10cm.将气缸倒过来放置,活塞下方的空气能通过平台上的缺口与大气相通,缓慢升高周围的温度到多少摄氏度时,封闭气柱的长为L2=18cm.g取l0m/s2,气缸足够长.
如图,导热性能良好的气缸放置在水平平台上,活塞质量m=10kg,横截面积S=50cm2,大气压强为p0=l×105Pa,当温度为t1=-3℃时,活塞封闭的气柱长L1=10cm.将气缸倒过来放置,活塞下方的空气能通过平台上的缺口与大气相通,缓慢升高周围的温度到多少摄氏度时,封闭气柱的长为L2=18cm.g取l0m/s2,气缸足够长.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,静止在水平桌面上的木块,在水平方向受到推力F1、F2和摩擦力f的作用.已知F1=10N,F2=2N,则木块受到的摩擦力大小和方向分别为( )
如图所示,静止在水平桌面上的木块,在水平方向受到推力F1、F2和摩擦力f的作用.已知F1=10N,F2=2N,则木块受到的摩擦力大小和方向分别为( )| A. | 8N 水平向右? | B. | 8N 水平向左 | C. | 10N 水平向右? | D. | 12N 水平向左 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
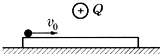 如图所示,在水平放置的光滑金属板中点的正上方,有带正电的点电荷Q.一表面绝缘、带正电的金属球(可视为质点,且不影响原电场)以速度v0开始在金属板上向右运动,在运动过程中( )
如图所示,在水平放置的光滑金属板中点的正上方,有带正电的点电荷Q.一表面绝缘、带正电的金属球(可视为质点,且不影响原电场)以速度v0开始在金属板上向右运动,在运动过程中( )| A. | 小球减速后作加速运动 | B. | 小球作匀速直线运动 | ||
| C. | 小球受电场力的冲量为零 | D. | 以上说法可能都不正确 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 1865年麦克斯韦提出光是电磁波的一种形态 | |
| B. | 1801年托马斯•杨在实验室成功观察到了光的衍射 | |
| C. | 1818年泊松通过实验发现了圆板衍射的“泊松亮斑” | |
| D. | 1905年爱因斯坦在广义相对论中提出光速不变原理 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com