
如图所示,两物体的质量分别为M和m(M>m),用细绳连接后跨在半径为R的固定光滑半圆柱体上,两物体刚好位于其水平直径的两端,释放后它们由静止开始运动,求m到达圆柱顶端时对圆柱顶端的压力.

|
对m和M及地球组成的系统,圆柱面对m的弹力不做功,只有重力对系统做功,系统的机械能守恒,据此可求出m运动到圆柱顶时的速度,从而可知道它在最高点时的向心加速度,由牛顿第二定律即可求出m受到的支持力. 取m,M的起始位置为重力势能零点,则系统初始位置的机械能E1=0. 设当m运动到圆柱顶时的速度为v,此时M向下移动
E2=mgR+(-Mg· 由机械能守恒有E1=E2,即
0=mgR-Mg· 由此解得
v2= 设m在圆柱顶时所受的支持力为N,由牛顿第二定律有
mg-N=m 所以
N=mg-m 根据牛顿第三定律,m对圆柱顶端的压力
|
|
对m和M组成的系统,内力做功代数和为零,因此系统机械能守恒.注意m上升的高度和M下降高度的不同,两者的速度都沿绳的方向,两者速度大小相等. |


科目:高中物理 来源: 题型:
 如图所示,两物体处于静止状态,它们的质量m1=2m2,它们与水平面间的动摩擦因数为μ2=2μ1,开始它们之间被细绳连接,并夹一压缩状态的轻质弹簧.当烧断细线后,两物体脱离弹簧时的速度均不为零,则下列结论正确的是( )
如图所示,两物体处于静止状态,它们的质量m1=2m2,它们与水平面间的动摩擦因数为μ2=2μ1,开始它们之间被细绳连接,并夹一压缩状态的轻质弹簧.当烧断细线后,两物体脱离弹簧时的速度均不为零,则下列结论正确的是( )查看答案和解析>>
科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,两物体处于静止状态,它们的质量m1=2m2,它们与水平间的动摩擦因数分别为μ1、μ2,且μ2=2μ1,开始它们之间被细绳连接,并夹一压缩状态的轻质弹簧,当烧断细线后,两物脱离弹簧时的速度均不为零,则( )
如图所示,两物体处于静止状态,它们的质量m1=2m2,它们与水平间的动摩擦因数分别为μ1、μ2,且μ2=2μ1,开始它们之间被细绳连接,并夹一压缩状态的轻质弹簧,当烧断细线后,两物脱离弹簧时的速度均不为零,则( )查看答案和解析>>
科目:高中物理 来源: 题型:
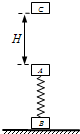 如图所示,两物体A、B分别与一竖直放置的轻质弹簧的两端相连接,B物体在水平地面上,A、B均处于静止状态.从A物体正上方与A相距H处由静止释放一小物体C.C与A相碰后立即粘在一起向下运动,以后不再分开.弹簧始终处于弹性限度内.用△E表示C与A碰撞过程中损失的机械能,用F表示C与A一起下落过程中地面对B的最大支持力.若减小C物体释放时与A物体间的距离H,其他条件不变,则( )
如图所示,两物体A、B分别与一竖直放置的轻质弹簧的两端相连接,B物体在水平地面上,A、B均处于静止状态.从A物体正上方与A相距H处由静止释放一小物体C.C与A相碰后立即粘在一起向下运动,以后不再分开.弹簧始终处于弹性限度内.用△E表示C与A碰撞过程中损失的机械能,用F表示C与A一起下落过程中地面对B的最大支持力.若减小C物体释放时与A物体间的距离H,其他条件不变,则( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com