
| A. | 赤道上物体与“三号卫星”的线速度之比为$\frac{{v}_{1}}{v3}$=$\sqrt{\frac{R+h}{R}}$ | |
| B. | 赤道上物体与近地卫星的角速度之比为$\frac{{ω}_{1}}{{ω}_{2}}$=$\sqrt{\frac{{R}^{3}}{(R+h)^{3}}}$ | |
| C. | 赤道上物体与“三号卫星”的向心加速度之比为$\frac{{a}_{1}}{{a}_{3}}$=$\frac{R}{(R+h)}$ | |
| D. | 近地卫星处与“三号卫星”处的重力加速之比为$\frac{{g}_{2}}{{g}_{3}}$=$\frac{(R+h)^{2}}{{R}^{2}}$ |
分析 “三号卫星”是地球同步卫星,其角速度与地球自转角速度相同,根据v=ωr分析赤道上物体与“三号卫星”的线速度之比.由a=ω2r分析赤道上物体与“三号卫星”的向心加速度之比.近地卫星的轨道半径可认为等于地球半径,根据万有引力提供向心力,可分析“三号卫星”与近地卫星的重力加速度的关系.
解答 解:A、赤道上物体与“三号卫星”的角速度相同,都等于地球自转角速度,根据v=ωr得:赤道上物体与“三号卫星”的线速度之比为$\frac{{v}_{1}}{v3}$=$\frac{R}{R+h}$.故A错误.
B、对于“三号卫星”与近地卫星,由万有引力提供向心力,得:
G$\frac{Mm}{{r}^{2}}$=mω2r
得:ω=$\sqrt{\frac{GM}{{r}^{3}}}$
可得“三号卫星”与近地卫星角速度之比为:
$\frac{ω{\;}_{3}}{ω{\;}_{2}}$=$\sqrt{\frac{{R}^{3}}{(R+h)^{3}}}$
又ω1=ω3,所以$\frac{{ω}_{1}}{{ω}_{2}}$=$\sqrt{\frac{{R}^{3}}{(R+h)^{3}}}$.故B正确.
C、赤道上物体与“三号卫星”的角速度相同,由a=ω2r分析得它们的向心加速度之比为$\frac{{a}_{1}}{{a}_{3}}$=$\frac{R}{(R+h)}$.故C正确.
D、对于“三号卫星”与近地卫星,由万有引力等于重力,得:
G$\frac{Mm}{{r}^{2}}$=mg
得:g=$\frac{GM}{{r}^{2}}$
所以得近地卫星处与“三号卫星”处的重力加速之比为$\frac{{g}_{2}}{{g}_{3}}$=$\frac{(R+h)^{2}}{{R}^{2}}$.故D正确.
故选:BCD
点评 解决本题时,要抓住研究对象相等的量,知道地球同步卫星的角速度等于赤道上物体的角速度.对于卫星,应根据万有引力等于向心力,以及万有引力等于重力,通过列式来分析.


科目:高中物理 来源: 题型:计算题
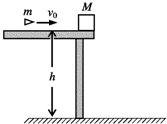 如图所示,一质量M=1.2kg的物块静止在桌面边缘.桌面离地面的高度h=1.8m,一质量m=20g的子弹以水平速度v0=200m/s射人物块,并在很短的时间内水平穿出,已知物块落地点离桌面边缘的水平距离x=1.2m,g取10m/s2.求:
如图所示,一质量M=1.2kg的物块静止在桌面边缘.桌面离地面的高度h=1.8m,一质量m=20g的子弹以水平速度v0=200m/s射人物块,并在很短的时间内水平穿出,已知物块落地点离桌面边缘的水平距离x=1.2m,g取10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:计算题

查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 根据玻尔原子结构理论,氦离子(He+)的能级图如图所示.当某个He+处在n=4的激发态时,由于跃迁所释放的光子不可能有( )
根据玻尔原子结构理论,氦离子(He+)的能级图如图所示.当某个He+处在n=4的激发态时,由于跃迁所释放的光子不可能有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 6个 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 图示为甲、乙两物体在同一条直线上运动的x-t图象,下列判断正确的是( )
图示为甲、乙两物体在同一条直线上运动的x-t图象,下列判断正确的是( )| A. | 甲、乙均做匀速直线运动 | |
| B. | 甲、乙两物体在t1时刻相遇 | |
| C. | 甲、乙两物体在同一时刻从同一位置出发 | |
| D. | 若t2=2t1,则甲、乙两物体在t2时刻的距离和它们在零时刻的距离相同 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
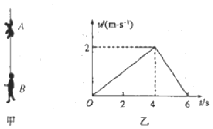 如图甲所示为杂技中的“顶竿”表演、水平地面上演员B用肩部顶住一根长直竹竿,另一演员A爬至竹竿顶端完成各种动作.某次顶竿表演结束后,演员A自竿顶由静止开始下落.滑到竿底时速度正好为零,然后曲腿跳到地面上,演员A、B质量均为50kg,长竹竿质量为5kg,A下滑的过程中速度随时间变化的图象如图乙所示.重力加速度g取10m/s2,下列判断正确的是( )
如图甲所示为杂技中的“顶竿”表演、水平地面上演员B用肩部顶住一根长直竹竿,另一演员A爬至竹竿顶端完成各种动作.某次顶竿表演结束后,演员A自竿顶由静止开始下落.滑到竿底时速度正好为零,然后曲腿跳到地面上,演员A、B质量均为50kg,长竹竿质量为5kg,A下滑的过程中速度随时间变化的图象如图乙所示.重力加速度g取10m/s2,下列判断正确的是( )| A. | 竹竿的总长度约为3m | |
| B. | 0-6s内,演员B对地面的压力大小始终为1050N | |
| C. | 0-6s内,竹竿对演员B的压力的冲量大小为3300N•s | |
| D. | 演员A落地时向下曲腿,是为了缩短作用时间以减小地面的冲击力 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
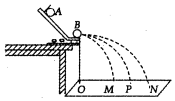 某同学用如图所示的装置做验证动量守恒定律的实验.先将A球从斜槽轨道上某固定点处由静止开始滚下,在水平地面上的记录纸上留下压痕,重复10次;再把同样大小的B球放在斜槽轨道末水平段的最右端上,让A球仍从同一固定点处由静止开始滚下,和B球相碰后,两球分别落在记录纸的不同位置处,重复10次.
某同学用如图所示的装置做验证动量守恒定律的实验.先将A球从斜槽轨道上某固定点处由静止开始滚下,在水平地面上的记录纸上留下压痕,重复10次;再把同样大小的B球放在斜槽轨道末水平段的最右端上,让A球仍从同一固定点处由静止开始滚下,和B球相碰后,两球分别落在记录纸的不同位置处,重复10次.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,间距为L平行且足够长的光滑导轨由两部分组成:倾斜部分与水平部分平滑相连,倾角为θ,在倾斜导轨顶端连接一阻值为r的定值电阻.质量为m、电阻也为r的金属杆MN垂直导轨跨放在导轨上,在倾斜导轨区域加以垂直导轨平面向下、磁感应强度为B的匀强磁场;在水平导轨区域加另一垂直轨道平面向下、磁感应强度也为B的匀强磁场.闭合开关S,让金属杆MN从图示位置由静止释放,已知金属杆运动到水平轨道前,已达到最大速度,不计导轨电阻且金属杆始终与导轨接触良好,重力加速度为g.求:
如图所示,间距为L平行且足够长的光滑导轨由两部分组成:倾斜部分与水平部分平滑相连,倾角为θ,在倾斜导轨顶端连接一阻值为r的定值电阻.质量为m、电阻也为r的金属杆MN垂直导轨跨放在导轨上,在倾斜导轨区域加以垂直导轨平面向下、磁感应强度为B的匀强磁场;在水平导轨区域加另一垂直轨道平面向下、磁感应强度也为B的匀强磁场.闭合开关S,让金属杆MN从图示位置由静止释放,已知金属杆运动到水平轨道前,已达到最大速度,不计导轨电阻且金属杆始终与导轨接触良好,重力加速度为g.求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题

| A. | 如图a,汽车通过拱桥的最高点处于超重状态 | |
| B. | 如图b所示是两个圆锥摆,增大θ,但保持圆锥的高度不变,则圆锥摆的角速度不变 | |
| C. | 如图c,同一小球在光滑而固定的圆锥筒内的A、B位置先后分别做匀速圆周运动,则在A、B两位置小球的角速度相等 | |
| D. | 如图c,同一小球在光滑而固定的圆锥筒内的A、B位置先后分别做匀速圆周运动,则在A、B两位置所受筒壁的支持力大小相等 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com