
| A. | 地球公转的周期及半径 | |
| B. | 月球绕地球运行的周期和运行的半径 | |
| C. | 人造卫星绕地球运行的周期 | |
| D. | 地球的半径 |
分析 根据万有引力提供向心力,结合轨道半径和周期(或线速度、角速度、向心加速度)求出中心天体的质量.
解答 解:A、已知地球公转的周期和半径,结合万有引力提供向心力可以求出太阳的质量,不能求出地球的质量,因为地球是环绕天体,质量被约去,无法求出,故A错误.
B、根据$G\frac{Mm}{{r}^{2}}=mr\frac{4{π}^{2}}{{T}^{2}}$得,已知月球的轨道半径和周期,可以求出地球的质量,故B正确.
C、已知人造卫星绕地球的周期,由于轨道半径未知,则无法求出地球的质量.故C错误.
D、已知地球的半径,密度未知,则无法求出地球的质量,故D错误.
故选:B.
点评 解决本题的关键掌握万有引力提供向心力这一重要理论,并能灵活运用,注意运用该理论只能求出中心天体的质量,无法得出环绕天体的质量.


 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案科目:高中物理 来源: 题型:选择题
| A. | $\frac{R-d}{R}$ | B. | $\frac{R}{R-d}$ | C. | ($\frac{R}{R-d}$)2 | D. | 1 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,在一平面M内放有一半径为R的半圆形导线,导线中所通的电流为I1,在半圆形导线的圆心O处垂直平面M固定一长直导线,导线中通以向上的电流I2,如图所示.已知长直导线在半圆形导线处产生的磁感应强度为B,则半圆形导线所受的安培力为( )
如图所示,在一平面M内放有一半径为R的半圆形导线,导线中所通的电流为I1,在半圆形导线的圆心O处垂直平面M固定一长直导线,导线中通以向上的电流I2,如图所示.已知长直导线在半圆形导线处产生的磁感应强度为B,则半圆形导线所受的安培力为( )| A. | 2BI1R | B. | 2BI2R | C. | πBI1R | D. | 0 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
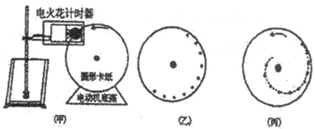
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | F=G$\frac{mM}{r^2}$=ma | B. | $\frac{R^3}{T^2}$ | ||
| C. | $\frac{{{R_地}^3}}{{{T_地}^2}}=\frac{{{R_月}^3}}{{{T_月}^2}}$ | D. | F=G$\frac{Mm}{r^2}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,一个倾角为α的直角斜面体静置于光滑水平面上,斜面体质量为M,顶端高度为h.今有一质量为m的小物体,沿光滑斜面下滑,当小物体从斜面顶端自由下滑到底端时,斜面体在水平面上移动的距离是( )
如图所示,一个倾角为α的直角斜面体静置于光滑水平面上,斜面体质量为M,顶端高度为h.今有一质量为m的小物体,沿光滑斜面下滑,当小物体从斜面顶端自由下滑到底端时,斜面体在水平面上移动的距离是( )| A. | $\frac{mh}{M+m}$ | B. | $\frac{Mh}{M+m}$ | C. | $\frac{mhcotα}{M+m}$ | D. | $\frac{Mhcotα}{M+m}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 甲物体在做加速运动,乙物体在做减速运动 | |
| B. | 甲、乙两物体的加速度方向相同 | |
| C. | 甲的加速度大于乙的加速度 | |
| D. | 甲、乙的速度量值都是越来越大 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com