
 如图所示,质量分别为M和m的物块与劲度系数为k的轻质弹簧两端相连,物块M放在地面上,用竖直向下的大小为F的恒力,压在物块m上,直到物块m运动至最低点时撤去恒力,此后物块m将向上运动.已知弹簧的弹性势能与形变量的关系为EP=$\frac{1}{2}$kx2.
如图所示,质量分别为M和m的物块与劲度系数为k的轻质弹簧两端相连,物块M放在地面上,用竖直向下的大小为F的恒力,压在物块m上,直到物块m运动至最低点时撤去恒力,此后物块m将向上运动.已知弹簧的弹性势能与形变量的关系为EP=$\frac{1}{2}$kx2.分析 (1)以m为研究的对象,对其进行受力分析,结合牛顿第二定律即可求出加速度;
(2)以m为研究的对象,对其进行受力分析,结合胡克定律,即可写出弹簧的弹力随位移变化的关系,最后作图;
(3)以整体为研究的对象,向求出M对地面的压力为0时,弹簧的长度,然后结合功能关系,即可求解.
解答 解:(1)用竖直向下的大小为F的恒力压在物块m上时,m受到重力、弹力和压力的作用处于平衡状态,所以弹簧的弹力:F1=F+mg
撤去压力的瞬间,弹簧的弹力来不及变化,所以m的加速度:$a=\frac{{F}_{1}-mg}{m}=\frac{F+mg-mg}{m}=\frac{F}{m}$;
(2)若施加的压力为0时,则m受到重力和弹簧的弹力的作用,则:F0=mg
随压力的增大,弹簧的弹力逐渐增大,F′=F+mg
由胡克定律:F1=k△x
可知,当压力为0时,弹簧的压缩量:${x}_{0}=\frac{{F}_{0}}{k}=\frac{mg}{k}$
当压力是F时,F1=F+mg
又弹簧的形变量△x与m的位移s关系为:△x=x0+s
所以,物块m下移过程中弹簧弹力与其位移关系:F1=k(x0+s)=mg+ks
的图象如图.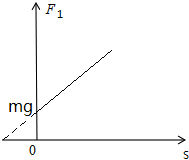
(3)要使下面的物块M不脱离地面,m受到的压力是F,弹簧的压缩量:$△{x}_{1}=\frac{{F}_{1}}{k}=\frac{F+mg}{k}$
此时弹簧的弹性势能:${E}_{P1}=\frac{1}{2}k△{x}_{1}^{2}=\frac{1}{2}k×(\frac{F+mg}{k})^{2}$=$\frac{(F+mg)^{2}}{2k}$
以M为研究的对象,当M刚刚要离开地面时,M受到弹簧的拉力和重力的作用,所以此时:F2=Mg,则弹簧的伸长量:$△{x}_{2}=\frac{{F}_{2}}{k}=\frac{Mg}{k}$
则此时弹簧的弹性势能:${E}_{P2}=\frac{1}{2}k△{x}_{2}^{2}=\frac{1}{2}×k×\frac{{M}^{2}{g}^{2}}{{k}^{2}}=\frac{{M}^{2}{g}^{2}}{2k}$
m上升的过程中,重力势能的增加量:△EP=mg(△x1+△x2)
弹簧上升的过程中,弹簧的弹性势能转化为m的重力势能,即:EP1-EP2=△EP
联立以上方程解得:F=(M+m)g
答:(1)物块m在最低点时的加速度是$\frac{F}{m}$;(2)如图;(3)要使下面的物块M不脱离地面,F的大小不能超过(M+m)g.
点评 本题将含有弹簧的平衡问题与功能关系结合振子一起,关键是分析两个状态弹簧的状态和弹力,再由几何关系研究A上升距离与弹簧形变量的关系.


科目:高中物理 来源: 题型:解答题
 如图所示,把一质量为0.5kg的电动玩具车,放在质量为1kg的带有光滑轮子的小车上,当接通玩具车的电源,使它相对与小车以0.5m/s的速度运动时,小车如何运动?
如图所示,把一质量为0.5kg的电动玩具车,放在质量为1kg的带有光滑轮子的小车上,当接通玩具车的电源,使它相对与小车以0.5m/s的速度运动时,小车如何运动?查看答案和解析>>
科目:高中物理 来源: 题型:选择题

| A. | mg | B. | mgtgθ | C. | $\frac{mg}{cosθ}$ | D. | mgcosθ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,在水平光滑的桌面上横放着一个圆筒,筒底固定着一个轻质弹簧,今有一小球沿水平方向正对弹簧射入筒内压缩弹簧,尔后又被弹出,取圆筒、弹簧、小球为系统,则系统在这一过程中( )
如图所示,在水平光滑的桌面上横放着一个圆筒,筒底固定着一个轻质弹簧,今有一小球沿水平方向正对弹簧射入筒内压缩弹簧,尔后又被弹出,取圆筒、弹簧、小球为系统,则系统在这一过程中( )| A. | 动量守恒,动能守恒 | B. | 动量守恒,机械能守恒 | ||
| C. | 动量不守恒,动能守恒 | D. | 动量不守恒,机械能守恒 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,当导线MN沿导轨开始向右滑动的瞬间(导轨间有磁场,磁场方向垂直纸面向里),正对电磁铁A的圆形金属环B中( )
如图所示,当导线MN沿导轨开始向右滑动的瞬间(导轨间有磁场,磁场方向垂直纸面向里),正对电磁铁A的圆形金属环B中( )| A. | 有感应电流 | B. | 没有感应电流 | ||
| C. | 可能有也可能没有感应电流 | D. | 条件不足,无法确定 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 倒置的光滑圆锥面内侧,有质量相同的两个小玻璃球A、B,沿锥面在水平面内作匀速圆周运动,关于A、B两球的角速度、线速度和向心加速度正确的说法是( )
倒置的光滑圆锥面内侧,有质量相同的两个小玻璃球A、B,沿锥面在水平面内作匀速圆周运动,关于A、B两球的角速度、线速度和向心加速度正确的说法是( )| A. | 它们的角速度相等ωA=ωB | B. | 它们的线速度υA>υB | ||
| C. | 它们的向心加速度相等 | D. | A球的向心力小于B球的向心力 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,倾角为θ的固定光滑斜面底部有一垂直斜面的固定挡板C,劲度系数为k1的轻弹簧两端分别与质量均为m的物体A和B连接,劲度系数为k2的轻弹簧一端与A连接,另一端通过一根轻绳与一轻质小桶P相连,跨过光滑的定滑轮Q放在斜面上,B靠在挡板C处,A和B均静止.现缓慢地向小桶P内加入细砂,当B与挡板C间挤压力恰好为零时,
如图所示,倾角为θ的固定光滑斜面底部有一垂直斜面的固定挡板C,劲度系数为k1的轻弹簧两端分别与质量均为m的物体A和B连接,劲度系数为k2的轻弹簧一端与A连接,另一端通过一根轻绳与一轻质小桶P相连,跨过光滑的定滑轮Q放在斜面上,B靠在挡板C处,A和B均静止.现缓慢地向小桶P内加入细砂,当B与挡板C间挤压力恰好为零时,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com