
 2015年12月,我国发射了一颗科学实验卫星.如图所示,该科学实验卫星绕地球
2015年12月,我国发射了一颗科学实验卫星.如图所示,该科学实验卫星绕地球| A. | 等于24小时 | B. | 等于地球同步卫星的周期 | ||
| C. | 小于地球同步卫星的周期 | D. | 大于地球同步卫星的周期 |
分析 根据万有引力提供向心力G$\frac{Mm}{{r}^{2}}$=m$\frac{4{π}^{2}}{{T}^{2}}$r,解出周期与轨道半径的关系,根据轨道半径的大小进行讨论.
解答 解:根据万有引力提供向心力有:G$\frac{Mm}{{r}^{2}}$=m$\frac{4{π}^{2}}{{T}^{2}}$r
得:T=2π$\sqrt{\frac{{r}^{3}}{GM}}$;
由于该科学实验卫星绕地球运行的轨道半径比地球同步卫星的轨道半径小,所以该科学实验卫星绕地球运行的周期,小于同步卫星的周期,故C正确,ABD错误.
故选:C
点评 本题要掌握万有引力提供向心力这个关系,要能根据题意选择恰当的向心力的表达式.


科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
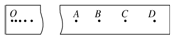 在“验证机械能守恒定律”的实验中,已知电磁打点计时器所用的电源的频率为50Hz,查得当地的重力加速度g=9.80m/s2,测得所用的重物质量为1.00kg.实验中得到一条点迹清晰的纸带(如图所示),把第一个点记作O,另选连续的四个点A、B、C、D作为测量的点,经测量知道A、B、C、D各点到O点的距离分别为62.99cm、70.18cm、77.76cm、85.73cm.
在“验证机械能守恒定律”的实验中,已知电磁打点计时器所用的电源的频率为50Hz,查得当地的重力加速度g=9.80m/s2,测得所用的重物质量为1.00kg.实验中得到一条点迹清晰的纸带(如图所示),把第一个点记作O,另选连续的四个点A、B、C、D作为测量的点,经测量知道A、B、C、D各点到O点的距离分别为62.99cm、70.18cm、77.76cm、85.73cm.查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,在小康和小红一起完成“测反应时间”的实验中,只要测量小康释放直尺到小红捏住直尺这段时间内直尺下落的高度h,利用重力加速度g,就能确定小红的反应时间t.则反应时间t的计算公式是( )
如图所示,在小康和小红一起完成“测反应时间”的实验中,只要测量小康释放直尺到小红捏住直尺这段时间内直尺下落的高度h,利用重力加速度g,就能确定小红的反应时间t.则反应时间t的计算公式是( )| A. | t=$\sqrt{\frac{h}{2g}}$ | B. | t=$\sqrt{\frac{2h}{g}}$ | C. | t=$\frac{h}{2g}$ | D. | t=$\frac{2h}{g}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,半径R=0.9m的光滑的半圆轨道固定在竖直平面内,直径AB竖直,下端A与光滑的水平轨道相切.一个质量m=1kg的小球沿水平轨道从A端以vA=3m/s的速度进入竖直圆轨道,小球恰好能通过最高点B,不计空气阻力,g取10m/s2.求:
如图所示,半径R=0.9m的光滑的半圆轨道固定在竖直平面内,直径AB竖直,下端A与光滑的水平轨道相切.一个质量m=1kg的小球沿水平轨道从A端以vA=3m/s的速度进入竖直圆轨道,小球恰好能通过最高点B,不计空气阻力,g取10m/s2.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com