
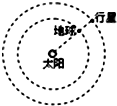
 某行星和地球绕太阳公转的轨道均可视为圆,每过N年,该行星会运行到日地连线的延长线上,如图所示,该行星与地球的公转半径比为( )
某行星和地球绕太阳公转的轨道均可视为圆,每过N年,该行星会运行到日地连线的延长线上,如图所示,该行星与地球的公转半径比为( )| A. | ($\frac{N}{N-1}$)${\;}^{\frac{2}{3}}$ | B. | ($\frac{N+1}{N}$)${\;}^{\frac{3}{2}}$ | C. | ($\frac{N}{N-1}$)${\;}^{\frac{3}{2}}$ | D. | ($\frac{N+1}{N}$)${\;}^{\frac{2}{3}}$ |
分析 由图可知行星的轨道半径大,那么由开普勒第三定律知其周期长,其绕太阳转的慢.每过N年,该行星会运行到日地连线的延长线上,说明N年地球比行星多转1圈,即行星转了N-1圈,从而再次在日地连线的延长线上,那么,可以求出行星的周期是$\frac{N}{N-1}$年,接着再由开普勒第三定律求解该行星与地球的公转半径比.
解答 解:由图可知行星的轨道半径大,那么由开普勒第三定律知其周期长.每过N年,该行星会运行到日地连线的延长线上,说明从最初在日地连线的延长线上开始,每一年地球都在行星的前面比行星多转圆周的N分之一,N年后地球转了N圈,比行星多转1圈,即行星转了N-1圈,从而再次在日地连线的延长线上.所以行星的周期是$\frac{N}{N-1}$年,
根据开普勒第三定律有:$\frac{{{r}_{地}}^{3}}{{{r}_{行}}^{3}}=\frac{{{T}_{地}}^{2}}{{{T}_{行}}^{2}}$,
则$\frac{{r}_{行}}{{r}_{地}}$=$\root{3}{\frac{{{T}_{行}}^{2}}{{{T}_{地}}^{2}}}$=($\frac{N}{N-1}$)${\;}^{\frac{2}{3}}$.
故选:A.
点评 解答此题的关键由题意分析得出每过N年地球比行星多围绕太阳转一圈,由此求出行星的周期,再由开普勒第三定律求解即可.


 期末集结号系列答案
期末集结号系列答案科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
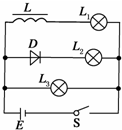 如图所示的电路中,三个灯泡L1、L2、L3的电阻关系为R1<R2<R3,电感L的电阻可忽略,D为理想二极管.电键S从闭合状态突然断开时,则下列判断正确的是( )
如图所示的电路中,三个灯泡L1、L2、L3的电阻关系为R1<R2<R3,电感L的电阻可忽略,D为理想二极管.电键S从闭合状态突然断开时,则下列判断正确的是( )| A. | L1立即熄灭 | B. | L2先变亮,然后熄灭 | ||
| C. | L3先变亮,然后熄灭 | D. | L2立即熄灭 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
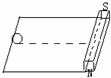 如图,一光滑的平面上,右方有一条形磁铁,一金属环以初速度V沿磁铁的中线向右滚动,则以下说法正确的是( )
如图,一光滑的平面上,右方有一条形磁铁,一金属环以初速度V沿磁铁的中线向右滚动,则以下说法正确的是( )| A. | 环的速度越来越小 | B. | 环保持匀速运动 | ||
| C. | 环的速度越来越大 | D. | 环的速度先增大后减小 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,质量分别为m和2m的A、B两物块由弹簧连接,静止在光滑的水平面上,弹簧为原长.现将质量为m,可视为质点的子弹以速度v0在极短时间内击中A并停留在其中.求:
如图所示,质量分别为m和2m的A、B两物块由弹簧连接,静止在光滑的水平面上,弹簧为原长.现将质量为m,可视为质点的子弹以速度v0在极短时间内击中A并停留在其中.求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 10-13N | B. | 10-9N | C. | 10-5 N | D. | 10-1N |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
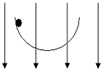 一个绝缘光滑半圆环轨道放在竖直向下的匀强电场中,场强为E,在环的上端,一个质量为m,带电量为+q的小球由静止开始沿轨道运动,则( )
一个绝缘光滑半圆环轨道放在竖直向下的匀强电场中,场强为E,在环的上端,一个质量为m,带电量为+q的小球由静止开始沿轨道运动,则( )| A. | 小球运动过程中机械能守恒 | B. | 小球运动的过程中机械能减少 | ||
| C. | 在最低点球对轨道的压力为(mg+Eq) | D. | 在最低点球对轨道的压力为3(mg+Eq) |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,B是质量为2m、半径为R的光滑半圆弧槽,放在光滑的水平桌面上.A是质量为3m的细长直杆,在光滑导孔的限制下,A只能上下运动.物块C的质量为m,紧靠B放置.初始时,A杆被夹住,使其下端正好与半圆弧槽内侧的上边缘接触,然后从静止释放A.求:
如图所示,B是质量为2m、半径为R的光滑半圆弧槽,放在光滑的水平桌面上.A是质量为3m的细长直杆,在光滑导孔的限制下,A只能上下运动.物块C的质量为m,紧靠B放置.初始时,A杆被夹住,使其下端正好与半圆弧槽内侧的上边缘接触,然后从静止释放A.求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 水平光滑直轨道ab与半径为R的竖直半圆形光滑轨道bc相切,一小球以初速度v0沿直轨道向右运动,如图所示,小球进入圆形轨道后刚好能通过c点,然后小球做平抛运动落在直轨道上的d点,则:
水平光滑直轨道ab与半径为R的竖直半圆形光滑轨道bc相切,一小球以初速度v0沿直轨道向右运动,如图所示,小球进入圆形轨道后刚好能通过c点,然后小球做平抛运动落在直轨道上的d点,则:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com