一列货车以v1=8m/s的恒定速度在平直铁路上运行,由于调度失误,在后面s0=600m处有一列快车以v2=20m/s的速度向它靠近,快车司机发觉后立即刹车做匀减速运动.已知快车以v2=20m/s的初速度做匀减速运动,要滑行s=2000m才停止.(不计司机的反应时间)
(1)试判断两车是否会发生相撞事故;
(2)若在快车刹车做匀减速运动的同时,货车以al=0.1m/s2的加速度加速行驶,则两车是否会发生相撞事故.
解:(1)快车刹车后做匀减速直线运动,初速度为v
0=20m/s,末速度v=0,位移x=2000m
则由v
2-
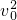
=2ax得a=

,所以快车刹车的加速度的大小为0.1m/s
2;
当快车速度减至与火车速度相等时,设运动时间为t
由t=

=120s
在这段时间内火车位移x
火=v
火t=8×120m=960m,快车的位移x
快=
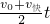
=1680m
因为x
快-x
火=1680-960=720m>700,所以两车会相撞.
(2)在快车刹车做匀减速运动的同时,货车以a
l=0.1m/s
2的加速度加速行驶,以货车为参考系,则快车做匀减速直线运动,加速度为:a′=a-a
1=0.2m/s
2,初速度为v′=v
2-v
1=12m/s,到相对静止过程,有

<600m
故不会相撞.
分析:(1)快车刹车后做匀减速直线运动,初速度为20m/s,运动位移为2000m时末速度为零,根据速度位移关系公式求出加速度;
快车做匀减速直线运动运动,货车做匀速直线运动,两车能否相撞看快车速度减到和货车相等时,快车的位移与货车的位移之差与距离600m的关系,大于或等于600m则不相撞,小于则相撞.
(2)以货车为参考系,快车仍然为匀减速直线运动,求出相对加速度与相对初速度,然后根据速度位移公式列式求解.
点评:本题是追击问题,判断两车能否相撞,不能以快车停下来通过的位移2000m来判断,而是根据两车速度相等时位移关系分析.

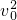 =2ax得a=
=2ax得a= ,所以快车刹车的加速度的大小为0.1m/s 2;
,所以快车刹车的加速度的大小为0.1m/s 2; =120s
=120s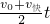 =1680m
=1680m <600m
<600m

 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案