
 如图所示,某皮带传动装置与水平面夹角为30°,两轮轴心相距L=2m,A、B分别是传送带与两轮的切点,传送带不打滑.现传送带沿顺时针方向以v=2.5m/s的速度匀速运动,将与小物块轻轻地放置于A点,小物块与传送带间的动摩擦因数为μ=$\frac{\sqrt{3}}{2}$,g取10m/s2.试求:
如图所示,某皮带传动装置与水平面夹角为30°,两轮轴心相距L=2m,A、B分别是传送带与两轮的切点,传送带不打滑.现传送带沿顺时针方向以v=2.5m/s的速度匀速运动,将与小物块轻轻地放置于A点,小物块与传送带间的动摩擦因数为μ=$\frac{\sqrt{3}}{2}$,g取10m/s2.试求:分析 (1)根据牛顿第二定律和运动学公式分析小物块的运动情况.先由牛顿第二定律求出小物块沿传送带向下匀加速运动的加速度,由运动学公式求出物块速度与传送带相等时所经过的时间和通过的位移,判断物块的速度与传动带速度相等以后物体的运动情况,再求解运动时间.
(2)小物块从A到B一直做匀加速直线运动,到达B点的速度最大;小物块从A到B一直做匀减速直线运动,到达B点的速度最小,根据位移速度关系求解速度大小,由此确定速度范围.
解答 解:(1)开始小物块受到竖直向下的重力、垂直传送带向上的支持力和沿传送带斜向上的摩擦力作用,做匀加速直线运动,设加速度为a1,根据牛顿第二定律可得:
μmgcos30°-mgsin30°=ma1,
代入数据解得:a1=2.5m/s2,
当小物块速度等于2.5m/s时,设小物块对地位移为L1,用时为t1,根据匀加速直线运动规律有:
t1=$\frac{{v}_{1}}{{a}_{1}}=\frac{2.5}{2.5}s=1s$,
L1=$\frac{{v}_{1}^{2}}{2{a}_{1}}=\frac{2.{5}^{2}}{2×2.5}m=1.25m$,
由于L1<L 且μ>tan30°,当小物块速度等于2.5m/s时,小物块将匀速直线运动至B点,
设用时为t2,根据匀速直线运动规律可得:${t}_{2}=\frac{L-{L}_{1}}{v}=0.3s$,
故小物块由静止出发从A到B所用时间为:t=t1+t2=1.3s;
(2)由于传送带的速度可以任意调节,则小物块从A到B一直做匀加速直线运动,到达B点的速度最大,
根据位移速度关系可得:${v}_{B}^{2}-{v}_{0}^{2}=2{a}_{1}L$,
代入数据解得:vB=8m/s;
小物块从A到B一直做匀减速直线运动,到达B点的速度最小,根据牛顿第二定律可得:
μmgcos30°+mgsin30°=ma2,
代入数据解得:a2=12.5m/s2,
由运动学公式可得:${v′}_{B}^{2}={v}_{0}^{2}-2{a}_{2}L$,
代入数据解得:vB′=2m/s;
即物块到达B点的速度范围为2m/s≤vB≤8m/s.
答:(1)小物块运动至B点的时间为1.3s;
(2)若传送带速度可以任意调节,当小物块在A点以v0=3$\sqrt{6}$m/s的速度沿传送带向上运动时,小物块到达B点的速度范围为2m/s≤vB≤8m/s.
点评 本题主要是考查了传送带问题,解决本题的关键理清物块的运动规律,结合牛顿第二定律和运动学公式综合求解.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中物理 来源:2016-2017学年甘肃会宁县一中高二文上期中考物理卷(解析版) 题型:填空题
到目前为止,科学实验发现的最小电荷量是电子所带的电荷量。这个最小电荷用e表示,它的数值为 。实验指出,所有带电物体的电荷量或者等于它,或者是它的整数倍数因此我们把它叫做 。
查看答案和解析>>
科目:高中物理 来源:2016-2017学年安徽师大附中高一上学期期中考物理试卷(解析版) 题型:选择题
历史上有些科学家曾把在相等位移内速度变化相等的单向直线运动称为“匀变速直线运动”(现称“另类匀变速直线运动”),“另类加速度”定义为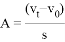 ,其中
,其中 和
和 分别表示某段位移
分别表示某段位移 内的初速度和末速度,
内的初速度和末速度,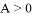 表示物体做加速运动,
表示物体做加速运动, 表示物体做减速运动。而现在物理学中加速度的定义式为
表示物体做减速运动。而现在物理学中加速度的定义式为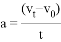 ,下列说法正确的是( )
,下列说法正确的是( )
A. 若A不变,则a也不变
B. 若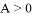 且保持不变,则a逐渐变大
且保持不变,则a逐渐变大
C. 若A不变,则物体在中间位置处的速度为
D. 若A不变,则物体在中间位置处的速度为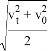
查看答案和解析>>
科目:高中物理 来源:2017届广东省韶关市六校高三10月联考物理试卷(解析版) 题型:填空题
某同学“验证牛顿第二定律”的实验装置如图所示,其中电源的频率为50Hz。

(1)她想用砂桶的重力表示小车受到的合外力F,为了减小这种做法带来的实验误差,她先做了两方面的调整措施:
a.用小木块将长木板无滑轮的一端垫高,目的是_____________.
b.使砂桶的质量远小于小车的质量,目的是使拉小车的力近似等于________________.
(2)实验中打出的其中一条纸带如图所示,由该纸带可求得小车的加速度a=________m/s2(结果保留两位有效数字)

查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,光滑导轨与水平面成α角,导轨宽L.有大小为B的匀强磁场,方向垂直导轨面,金属杆长为L,质量为m,水平放在导轨上.当回路中通过电流时,金属杆正好能静止.求:电流的大小为多大?磁感应强度的方向如何?
如图所示,光滑导轨与水平面成α角,导轨宽L.有大小为B的匀强磁场,方向垂直导轨面,金属杆长为L,质量为m,水平放在导轨上.当回路中通过电流时,金属杆正好能静止.求:电流的大小为多大?磁感应强度的方向如何?查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 水平放置的U形金属框架中接有电源,电动势为ε,内阻为r.框架上放置一质量为m,电阻为R的金属杆,它可以在框架上无摩擦的滑动,框架两边相距为L,匀强磁场的磁感强度为B,方向竖直向上.当ab杆受到水平向右足够大的恒力F时,求:
水平放置的U形金属框架中接有电源,电动势为ε,内阻为r.框架上放置一质量为m,电阻为R的金属杆,它可以在框架上无摩擦的滑动,框架两边相距为L,匀强磁场的磁感强度为B,方向竖直向上.当ab杆受到水平向右足够大的恒力F时,求:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 电场中某区域的电场线如图,在P点放置电量q1=+4.0×10-5C的点电荷,受到的电场力大小为F=0.2N,方向为水平向右.求:
电场中某区域的电场线如图,在P点放置电量q1=+4.0×10-5C的点电荷,受到的电场力大小为F=0.2N,方向为水平向右.求:查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示是质谱仪的工作原理示意图.设法使某种电荷量为q的正离子导入容器A中,离子再从狭缝S1飘入电压为U的加速电场,初速度不计.再通过狭缝S2、S3射入磁感应强度为B的匀强磁场中,射入方向垂直于磁场区的界面PQ.最后离子打到感光片上,形成垂直于纸面且平行于狭缝S3的细线.若测得细线到狭缝S3的距离为d,请导出离子的质量m的表达式.
如图所示是质谱仪的工作原理示意图.设法使某种电荷量为q的正离子导入容器A中,离子再从狭缝S1飘入电压为U的加速电场,初速度不计.再通过狭缝S2、S3射入磁感应强度为B的匀强磁场中,射入方向垂直于磁场区的界面PQ.最后离子打到感光片上,形成垂直于纸面且平行于狭缝S3的细线.若测得细线到狭缝S3的距离为d,请导出离子的质量m的表达式.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com