
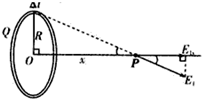
 现在我们要研究有关电场强弱的问题:
现在我们要研究有关电场强弱的问题:分析 (1)由电场强度大小的公式直接判断;
(2)求出圆环的周长,再计算△l的圆弧长的电量;
利用勾股定理得出点P的距离的平方,把△l的圆弧长的电量代入电场强度公式E=$\frac{kq}{{r}^{2}}$,可得P点的产生的电场强度的大小;
利用三角形余弦公式计算出E1沿着OP方向的分量E1x;最后EP的大小是E1x×$\frac{2πR}{△l}$,从而即可一一求解.
解答 解:(1)根据题意可知,电场强度大小公式E=$\frac{kq}{{r}^{2}}$,可知,当r增大时,E变小,所以距离带电体越远的,电场强度越弱;
(2)半径为R的圆环的周长是2πR,圆弧长度为△l弧上的电量为Q′=$\frac{Q}{2πR}×△l$=$\frac{Q•△l}{2πR}$,
由股定理可知,△l处到点P的距离的平方,r2=R2+x2,
因此P点所产生电场强度的大小为E1=$\frac{kq}{{r}^{2}}$=k×$\frac{\frac{Q•△l}{2πR}}{{R}^{2}+{x}^{2}}$=$\frac{kQ•△l}{2πR({R}^{2}+{x}^{2})}$,
根据cos∠E1PE1x=$\frac{x}{({R}^{2}+{x}^{2})^{\frac{1}{2}}}$
所以E1沿着OP方向的分量E1x=E1cos∠E1PE1x=$\frac{kQx•△l}{2πR({R}^{2}+{x}^{2})^{\frac{3}{2}}}$
那么EP的大小是EP=E1x×$\frac{2πR}{△l}$=$\frac{kQx•△l}{2πR({R}^{2}+{x}^{2})^{\frac{3}{2}}}$×$\frac{2πR}{△l}$=$\frac{kxQ}{({R}^{2}+{x}^{2})^{\frac{3}{2}}}$
故答案为:(1)弱;(2)$\frac{Q•△l}{2πR}$,$\frac{kQ•△l}{2πR({R}^{2}+{x}^{2})}$,$\frac{kQx•△l}{2πR({R}^{2}+{x}^{2})^{\frac{3}{2}}}$,$\frac{kxQ}{({R}^{2}+{x}^{2})^{\frac{3}{2}}}$.
点评 考查点电荷电场强度的公式内容,掌握矢量的合成与分解,理解三角知识的应用,注意正确的数学公式运算是解题的难点.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中物理 来源: 题型:选择题
| A. | 向心加速度越小 | B. | 角速度越小 | C. | 线速度越小 | D. | 周期越小 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
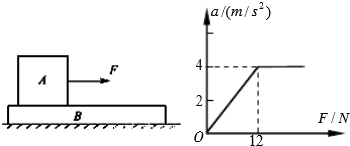
| A. | 当F<12N时,A、B都相对地面静止 | |
| B. | 当F>12N时,A相对B发生滑动 | |
| C. | 当a=2m/s2时,A与B之间的摩擦力为4 N | |
| D. | 当F=16N时,A的加速度为6 m/s2 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 在光滑圆锥形容器中,固定了一根光滑的竖直细杆,细杆与圆锥的中轴线重合,细杆上穿有小环(小环可以自由转动,但不能上下移动),小环上连接一轻绳,与一质量为m的光滑小球相连,让小球在圆锥内做水平面上的匀速圆周运动,并与圆锥内壁接触.如图所示,图①中小环与小球在同一水平面上,图②中轻绳与竖直轴成θ角.设图①和图②中轻绳对小球的拉力分别为Ta和Tb,圆锥内壁对小球的支持力分别为Na和Nb,则下列说法中正确的是( )
在光滑圆锥形容器中,固定了一根光滑的竖直细杆,细杆与圆锥的中轴线重合,细杆上穿有小环(小环可以自由转动,但不能上下移动),小环上连接一轻绳,与一质量为m的光滑小球相连,让小球在圆锥内做水平面上的匀速圆周运动,并与圆锥内壁接触.如图所示,图①中小环与小球在同一水平面上,图②中轻绳与竖直轴成θ角.设图①和图②中轻绳对小球的拉力分别为Ta和Tb,圆锥内壁对小球的支持力分别为Na和Nb,则下列说法中正确的是( )| A. | Ta一定为零,Tb一定为零 | B. | Ta可以为零,Tb可以为零 | ||
| C. | Na一定不为零,Nb可以为零 | D. | Na可以为零,Nb可以为零 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
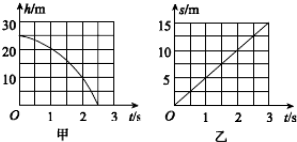
| A. | 物体抛处的初速度为5m/s | B. | 物体落地时的速度为20m/s | ||
| C. | 星球表面的重力加速度为8m/s2 | D. | 物体受到星球的引力大小为8N |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
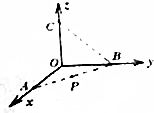 如图所示,在空间坐标系中存在匀强电场,A、B、C分别是x、y、z轴上到原点距离相等的三个点,P为AB连线中点,已知电场线平行于BC连线,B点电势为3V,C点电势为-3V,则电荷量为2.0×10-6C的带正电粒子从O点运动到P点,电场力所做的功为( )
如图所示,在空间坐标系中存在匀强电场,A、B、C分别是x、y、z轴上到原点距离相等的三个点,P为AB连线中点,已知电场线平行于BC连线,B点电势为3V,C点电势为-3V,则电荷量为2.0×10-6C的带正电粒子从O点运动到P点,电场力所做的功为( )| A. | 6.0×10-6J | B. | -3.0×10-6J | C. | -2.0×10-6J | D. | 1.5×10-6J |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 这两个力可能同时都能做正功 | |
| B. | 这两个力可能同时都能做负功 | |
| C. | 如果其中一个力做功为1J,则另一个力做功一定为-1J | |
| D. | 如果其中一个力不做功,则另一个力也不做功 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 一列简谐横波在t=0时刻的波形如图所示,质点P此时刻沿y轴负方向运动,经过0.1s第一次到达平衡位置,波速为5m/s,求:
一列简谐横波在t=0时刻的波形如图所示,质点P此时刻沿y轴负方向运动,经过0.1s第一次到达平衡位置,波速为5m/s,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com