
 如图,足够长的光滑斜面倾角θ=37°,两个物块A,B质量均为m,用劲度系数为k的轻质弹簧连接,C为固定在斜面上的挡板,物块A通过一根轻绳跨过光滑定滑轮与物块D相连,用手托住D,使轻绳伸直但没有弹力,将D由静止释放,运动中D始终未落地,不考虑空气阻力,问:
如图,足够长的光滑斜面倾角θ=37°,两个物块A,B质量均为m,用劲度系数为k的轻质弹簧连接,C为固定在斜面上的挡板,物块A通过一根轻绳跨过光滑定滑轮与物块D相连,用手托住D,使轻绳伸直但没有弹力,将D由静止释放,运动中D始终未落地,不考虑空气阻力,问:分析 (1)A和D下降的过程中,先做加速运动,后做减速运动,由于弹簧的弹力与弹簧的形变量成正比,所以A和D的加速过程和减速过程是对称的,当它们的速度是0时,加速度的方向与开始时加速度的方向相反,结合B恰好不离开C时对C的压力恰好为0,即可得出D的质量满足的条件;
(2)若D的质量为也m,B离开C时,A与D的重力势能的变化等于它们动能的增加,然后求出D的速率;
(3)结合概念关系即可求出D下落的最大速度v最大.
解答 解:(1)没有松开手之前,A处于平衡状态,沿斜面的方向弹簧的弹力与A受到的重力的分力大小相等,得:F=mgsin
设D的质量为M,则A与D刚刚开始运动时,A与D的加速度的方向都沿绳子的方向,D侧向下,由牛顿第二定律得:
Mg-mgsinθ+F=(M+m)a
所以:$a=\frac{Mg}{M+m}$ ①
B恰好不离开C时对C的压力恰好为0,以B为研究的对象,则沿斜面方向:F′=mgsinθ ②
A和D下降的过程中,先做加速运动,后做减速运动,由于弹簧的弹力与弹簧的形变量成正比,所以A和D的加速过程和减速过程是对称的,当它们的速度是0时,加速度的方向与开始时加速度的方向相反,由牛顿第二定律得:F′+mgsinθ-Mg=(m+M)a ③
联立①②③得:M=msinθ=m×sin37°=0.6m
(2)由(1)的解答过程可知,B刚刚要离开C时,弹簧的拉力与开始时弹簧的拉力大小相等,所以B刚刚要离开C时,弹簧的弹性势能与开始时弹簧的弹性势能相等,A与D的重力势能的变化等于它们动能的增加.
开始时:F=mgsinθ=kx1
B刚刚要离开C时:F′=mgsinθ=kx2
D下降的高度:${h}_{1}={x}_{1}+{x}_{2}=\frac{2mgsinθ}{k}=\frac{1.2mg}{k}$④
A上升的高度:${h}_{2}=({x}_{1}+{x}_{2})sinθ=\frac{2mgsi{n}^{2}θ}{k}=\frac{0.72mg}{k}$ ⑤
由机械能守恒得:$mg{h}_{1}-mg{h}_{2}=\frac{1}{2}•2m{v}^{2}$ ⑥
联立④⑤⑥得:$v=0.4g\sqrt{\frac{3m}{k}}$
(3)若D的质量为$\frac{m}{2}$,D达到速度最大时A与D受到的合外力为0,设此时弹簧的弹力为F″,则:$mgsinθ-F″-\frac{1}{2}mg=0$
得:F″=0.1mg
又:F″=kx3
得:${x}_{3}=\frac{F″}{k}=\frac{0.1mg}{k}$ ⑧
D下降的高度:${h}_{3}={x}_{1}-{x}_{3}=\frac{mgsinθ-0.1mg}{k}=\frac{0.5mg}{k}$ ⑨
A上升的高度${h}_{4}={(x}_{1}-{x}_{3})sinθ=\frac{0.3mg}{k}$ (10)
由机械能守恒得:$\frac{1}{2}mg{h}_{3}-mg{h}_{4}+△{E}_{P}=\frac{1}{2}•(\frac{1}{2}m+m){v}_{m}^{2}$ (11)
联立以上三式得:${v}_{m}=g•\sqrt{\frac{m}{10k}}$
答:(1)要使B不离开C,D的质量是0.6m;
(2)若D的质量为也m,B离开C时D的速率是$0.4g\sqrt{\frac{3m}{k}}$;
(3)若D的质量为$\frac{m}{2}$,已知D从释放到速度最大的过程中弹簧弹性势能的减少量△EP=$\frac{7{m}^{2}{g}^{2}}{40k}$,D下落的最大速度是$g•\sqrt{\frac{m}{10k}}$.
点评 本题过程较繁杂,涉及功能关系多,有弹性势能、重力势能等之间的转化,全面考察了学生综合分析问题能力和对功能关系的理解及应用,难度较大.对于这类题目在分析过程中,要化繁为简,即把复杂过程,分解为多个小过程分析,同时要正确分析受力情况,弄清系统运动状态以及功能关系.


科目:高中物理 来源: 题型:解答题
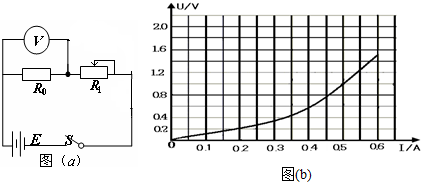
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
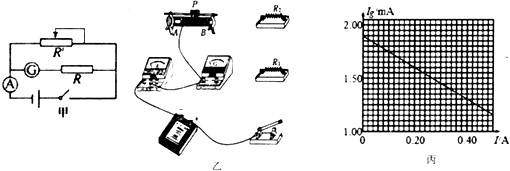
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | $\frac{{E}_{k}}{5}$ | B. | $\frac{2{E}_{k}}{5}$ | C. | $\frac{{E}_{k}}{2}$ | D. | $\frac{4{E}_{k}}{5}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
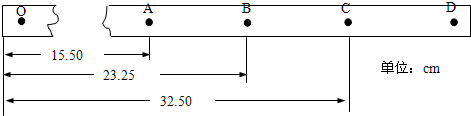
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
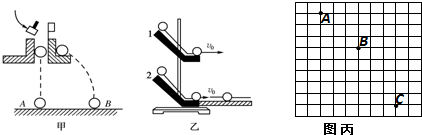
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com