
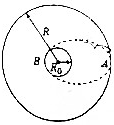
 �ɴ��ذ뾶ΪR��Բ�ι���Ƶ���������Բ���˶������Ҫ���ص����ڹ����ijһ��A���������ʣ��Ӷ�ʹ�ɴ������Ե���Ϊ�������Բ����˶�����Բ�������������B�����У���ͼ��ʾ����֪����뾶ΪR0�����������������ٶ�Ϊg��������˵����ȷ���ǣ�������
�ɴ��ذ뾶ΪR��Բ�ι���Ƶ���������Բ���˶������Ҫ���ص����ڹ����ijһ��A���������ʣ��Ӷ�ʹ�ɴ������Ե���Ϊ�������Բ����˶�����Բ�������������B�����У���ͼ��ʾ����֪����뾶ΪR0�����������������ٶ�Ϊg��������˵����ȷ���ǣ�������| A�� | �ɴ���A���������ʱ��Ҫ���� | |
| B�� | �ɴ��ڴ�A��B�˶��Ĺ����л�е������С�� | |
| C�� | �ɴ���A��������ʺ�����ʿ��ܴ��ڵ�һ�����ٶ� | |
| D�� | �ɴ���A���˶���B������Ҫ��ʱ��t=$\frac{�У�R+{R}_{0}��}{2{R}_{0}}\sqrt{\frac{R+{R}_{0}}{2g}}$ |
���� ��һ�����ٶ��ǽ��������ǵ������ٶȣ�Ҳ�����Ļ����ٶȣ��ڶ������ٶ���������������������ٶȣ�����������������������������ʵı仯�����жϻ�е�ܵı仯��
��� �⣺A���ɴ���A���������ʱ��Ҫ���ٽ��������˶�����A����
B���ɴ��ڴ�A��B�˶��Ĺ�����ֻ��������������е�����غ㣬��B����
C������G$\frac{Mm}{{r}_{\;}^{2}}=m\frac{{v}_{\;}^{2}}{r}$��$v=\sqrt{\frac{GM}{r}}$������뾶ԽС���ٶ�Խ������뾶��С���ڵ���뾶ʱ���ٶȵ��ڵ�һ�����ٶȣ�����һλ�����ƾ���Զ�ص��Բ�����Բ���˶���������ǵ��ٶ�һ��С�ڵ�һ�����ٶȣ���C����
D���ɴ��ڰ뾶ΪR��Բ����������Բ���˶�G$\frac{Mm}{{R}_{\;}^{2}}=m\frac{4{��}_{\;}^{2}}{{T}_{\;}^{2}}R$���ã�$T=\sqrt{\frac{4{��}_{\;}^{2}{R}_{\;}^{3}}{GM}}$����
�ڵ�������������������������У�$mg=G\frac{Mm}{{R}_{0}^{2}}$����
$T=\sqrt{\frac{4{��}_{\;}^{2}{R}_{\;}^{3}}{g{R}_{0}^{2}}}$��
����Բ������˶���T����ݿ����յ��������У�$\frac{{R}_{\;}^{3}}{{T}_{\;}^{2}}=\frac{��\frac{R+{R}_{0}^{\;}}{2}��_{\;}^{3}}{{T}_{\;}^{��2}}$��
�ã�$T��=\sqrt{\frac{��R+{R}_{0}^{\;}��_{\;}^{3}}{8{R}_{\;}^{3}}}T=��\sqrt{\frac{��R+{R}_{0}^{\;}��_{\;}^{3}}{2g{R}_{0}^{2}}}$=$\frac{�У�R+{R}_{0}^{\;}��}{{R}_{0}^{\;}}\sqrt{\frac{R+{R}_{0}^{\;}}{2g}}$
�ɴ���A�㵽B������ʱ��Ϊ��$t=\frac{T��}{2}=\frac{�У�R+{R}_{0}^{\;}��}{2{R}_{0}^{\;}}\sqrt{\frac{R+{R}_{0}^{\;}}{2g}}$����D��ȷ
��ѡ��D
���� ��������Ӧ������ͨ��Ҫץס�����ṩ��������ʽ��⣬ͬʱ����Ҫץס�ɴ���������뾶�Ĺ�ϵ���з�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
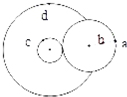 ��ͼ�����ִ���װ�������ְ뾶Ϊ2r��aΪ����Ե�ϵ�һ�㣬bΪ���ϵ�һ�㣬b����Ϊr�����Ϊһ���ᣬ���ֵİ뾶Ϊ4r��dΪ����Ե�ϵ�һ�㣻С�ְ뾶Ϊr��cΪ����Ե�ϵ�һ�㣮�������п��ֲ���������˵��������ǣ�������
��ͼ�����ִ���װ�������ְ뾶Ϊ2r��aΪ����Ե�ϵ�һ�㣬bΪ���ϵ�һ�㣬b����Ϊr�����Ϊһ���ᣬ���ֵİ뾶Ϊ4r��dΪ����Ե�ϵ�һ�㣻С�ְ뾶Ϊr��cΪ����Ե�ϵ�һ�㣮�������п��ֲ���������˵��������ǣ�������| A�� | c����d������ٶȴ�С֮��Ϊ1��4 | B�� | b����c�������֮��Ϊ1��1 | ||
| C�� | a����b��Ľ��ٶ�֮��Ϊ1��1 | D�� | a����c������ٶ�֮��Ϊ1��1 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
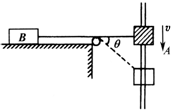 ��ͼ��ʾ����ʼʱA��B���ϸ����ˮƽ״̬����ʹ����A���ٶ�v�ظ������»�����ϸ��ͨ��������������B��������ˮƽ����ļн�Ϊ��ʱ������B���ٶ�Ϊ��������
��ͼ��ʾ����ʼʱA��B���ϸ����ˮƽ״̬����ʹ����A���ٶ�v�ظ������»�����ϸ��ͨ��������������B��������ˮƽ����ļн�Ϊ��ʱ������B���ٶ�Ϊ��������| A�� | vcos�� | B�� | vsin�� | C�� | $\frac{v}{cos��}$ | D�� | $\frac{v}{sin��}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ���������ֱ汾���ǿ | B�� | ���������ֱ汾���ǿ | ||
| C�� | ���������ֱ汾����ͬ | D�� | ���������ֱ汾�첻��Ƚ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | PM2.5��������˶������������ķ��������˶��ķ�ӳ | |
| B�� | ֻҪŬ�������ŵ�һ�����������ջ����Ƴɹ��� | |
| C�� | �����¶�ÿ����1�棬��Ӧ������ѧ�¶�Ҳ������1K | |
| D�� | ���ܲ�ͬ�����壬���Ƿ������˶���ƽ�����ܿ�����ͬ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ�������ͬһƽ����MNֱ���Ϲ̶�������ֱ�Ϊ-9Q��+Q���������ɣ��������ΪL����+Q����ΪԲ�ģ��뾶Ϊ $\frac{L}{2}$ ��Բ��a��b��c��d��Բ�����ĵ㣬����a��b��MNֱ���ϣ�c��d�������ߴ�ֱ��MN��һ�����Ϊq�ĸ�������Բ�����˶����Ƚ�a��b��c��d�ĵ㣬������˵��������ǣ�������
��ͼ��ʾ�������ͬһƽ����MNֱ���Ϲ̶�������ֱ�Ϊ-9Q��+Q���������ɣ��������ΪL����+Q����ΪԲ�ģ��뾶Ϊ $\frac{L}{2}$ ��Բ��a��b��c��d��Բ�����ĵ㣬����a��b��MNֱ���ϣ�c��d�������ߴ�ֱ��MN��һ�����Ϊq�ĸ�������Բ�����˶����Ƚ�a��b��c��d�ĵ㣬������˵��������ǣ�������| A�� | ��a��糡ǿ����� | B�� | ���q��b��ĵ�������� | ||
| C�� | ��c��d����ĵ������ | D�� | ���q��a��ĵ�������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ����ƹ��Ϊʹƹ�����ڱ����е����ش������ӣ���߱����Ĺ����ԣ������������ֱ����ԭ����38mm����40mm��������ԭ����2.5�����ӵ�2.7�ˣ��о���Ա�ƣ�40mm�����ԭ38mmС����ת����$\frac{1}{5}$���ٶȼ���$\frac{1}{7}$������Ҳ�����½���С��Ϊ�˱Ƚ��¡��ϱ�ƹ������˶����ԣ�������һͬѧ��һֱֻ��40mm�Ĵ����һֱֻ��38mm��С��ͬһ�ߴ�ͬʱ�������£���������������У�������������㵽�������������һ�ξ�������Ƭ����ͼ��ʾ�������еĺ���������ֱǽ���������ש�Ľӷ괦������ʱ���ÿ����ٶ�Ϊ$\frac{1}{30}$�룬��
����ƹ��Ϊʹƹ�����ڱ����е����ش������ӣ���߱����Ĺ����ԣ������������ֱ����ԭ����38mm����40mm��������ԭ����2.5�����ӵ�2.7�ˣ��о���Ա�ƣ�40mm�����ԭ38mmС����ת����$\frac{1}{5}$���ٶȼ���$\frac{1}{7}$������Ҳ�����½���С��Ϊ�˱Ƚ��¡��ϱ�ƹ������˶����ԣ�������һͬѧ��һֱֻ��40mm�Ĵ����һֱֻ��38mm��С��ͬһ�ߴ�ͬʱ�������£���������������У�������������㵽�������������һ�ξ�������Ƭ����ͼ��ʾ�������еĺ���������ֱǽ���������ש�Ľӷ괦������ʱ���ÿ����ٶ�Ϊ$\frac{1}{30}$�룬���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{4{��^2}{r^3}}}{{G{T^2}}}$ | B�� | $\frac{{3��{R^3}}}{{G{T^2}{r^3}}}$ | C�� | $\frac{{3��{r^3}}}{{G{T^2}{R^3}}}$ | D�� | $\frac{3��}{{G{T^2}}}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com