
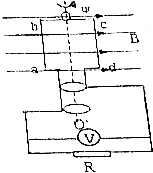
 ��ͼ��ʾ�����������ģ�͵���������Ȧabcd����ǿ�ų��У���OO��������ת������Ȧ����N=100�ѣ��߳�ab=bc=10cm����Ȧ����Ϊr=1�������·����ΪR=9�����Ÿ�Ӧǿ����B=0.1T����Ȧת����n=10r/s����
��ͼ��ʾ�����������ģ�͵���������Ȧabcd����ǿ�ų��У���OO��������ת������Ȧ����N=100�ѣ��߳�ab=bc=10cm����Ȧ����Ϊr=1�������·����ΪR=9�����Ÿ�Ӧǿ����B=0.1T����Ȧת����n=10r/s�������� ��1���������ֶ������ȷ�����ķ���
��2�����ݸ�Ӧ�綯�����ֵ����ʽ������ֵ�����ɽ��ٶȹ�ʽ�����ٶȣ������ȷ��Ӧ�ı���ʽ��
��3�����ݼнǹ�ϵ����ö�Ӧ��˲ʱֵ��
��4���������ֵ����Чֵ֮��Ĺ�ϵ�������Чֵ������ŷķ���ɿ���õ�ѹ����ʾ����
��5�����ݹ��ʹ�ʽ����ù��ʣ�
��6����������ת������ȷ�����Ĺ��������ܵ����������ɽ������ɿ���������Ĺ���
��7������ƽ���綯�ƿ���õ��������ɵ�����ʽ����õ�����
��� �⣺��1��ͼʾλ��ʱ��ab��cd�и�Ÿ��ߣ������ֶ����֪����������Ϊabcd����
��2����Ȧת���Ľ��ٶ�Ϊ����=2��n=2�С�10=20��rad/s��
�綯�Ƶ����ֵΪ��Em=NBS��=100��0.1��0.1��0.1��2�С�10=2��V��
�������濪ʼ��ʱ���ʱ���ʽΪ��e=2��sin20��t
��3����Ȧ��Ÿ��н�Ϊ30��ʱ���൱����Ȧ������ת��60��ʱ�ĵ綯�ƣ����У�e=2�С�sin60��=$\sqrt{3}$��V��
��4����ѹ����ʾ��ΪR���˵�ѹ����Чֵ���У�U=$\frac{{E}_{m}}{\sqrt{2}��R+r��}R$=$\frac{2��}{\sqrt{2}}��\frac{9}{9+1}$=$\frac{9\sqrt{2}}{10}$��V=4.0V
��5��R�ϵ��ȹ���Ϊ��P=$\frac{{U}^{2}}{R}$=$\frac{4��{0}^{2}}{9}$=1.8W��
��6����Ȧת��һ��ʱ�����������Ĺ�������Ȧ�в��������������У�
E=I2��R+r��T=��$\frac{E}{r+R}$��2��R+r����$\frac{1}{n}$=��$\frac{2��}{\sqrt{2}��9+1��}$��2����9+1����$\frac{1}{10}$=0.2J��
��7��ת��90��ʱ��ͨ���ı仯Ϊ��
����=BS��
ƽ���綯��Ϊ��$\overline{E}$=$\frac{n����}{��t}$=$\frac{nBS}{��t}$
��ͨ���ĵ���Ϊ��q=It=$\frac{nBS}{��r+R��}$=$\frac{100��0.1��0.1��0.1}{10}$=0.01C
�𣺣�1����ͼ��ʾʱ��Ȧ�ϸ�Ӧ�����ķ���Ϊabcd��
��2���������濪ʼ��ʱ����Ӧ�綯�Ƶ�˲ʱֵ����ʽe=2��sin20��t
��3����Ȧƽ����Ÿ��н�Ϊ30��ʱ�ĸ�Ӧ�綯�ƵĴ�СΪ$\sqrt{3}$��V��
��4��ת�������е�ѹ���Ķ���Ϊ4.0V
��5������R�ϲ������ȹ���Ϊ1.8W
��6����Ȧÿתһ�ܣ��������Ĺ�Ϊ0.2J
��7����ͼʾλ�ÿ�ʼ����Ȧת��90��ǵĹ�����ͨ������r�ĵ���Ϊ0.01C��
���� ���⿼�齻�����е����м��㣬Ҫע����ȷ�������������ѹ������ʱҪ����Чֵ����������ʱҪ��ƽ��ֵ��ע�����ֵ����Чֵ֮��Ĺ�ϵ��


 ͬ����ϰǿ����չϵ�д�
ͬ����ϰǿ����չϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ���ʵ�λ���У���ѧ��Χ�ڣ��涨�Ļ������ǣ�ǧ�ˣ��ף��� | |
| B�� | ����Ϊ6�棬���е�λ��Ϊ���ʵ�λ�е�����ѧ�¶ȵĵ�λ | |
| C�� | �������Ķ���ʽ�ǣ�B=$\frac{F}{IL}$����B�ĵ�λ��$\frac{kg}{{A{s^2}}}$ | |
| D�� | ���F=G•$\frac{{{m_i}{m_2}}}{r^2}$����ȷ�ģ����������G�ĵ�λΪ��N•$\frac{m^2}{{k{g^2}}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
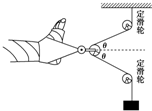 ��ͼ�ǹ��۲��˵�ǣ��װ��ʾ��ͼ������һ�˹̶����ƹ������ֺͶ����ֺ����һ������붯���������ķ��������Ų��˵Ľţ�����װ����ͬһ��ֱƽ���ڣ�Ϊ��ʹ�����ܵ��������ɲ�ȡ�ķ����ǣ�������
��ͼ�ǹ��۲��˵�ǣ��װ��ʾ��ͼ������һ�˹̶����ƹ������ֺͶ����ֺ����һ������붯���������ķ��������Ų��˵Ľţ�����װ����ͬһ��ֱƽ���ڣ�Ϊ��ʹ�����ܵ��������ɲ�ȡ�ķ����ǣ�������| A�� | ֻ�������ij��� | B�� | ֻ������������� | ||
| C�� | ֻ�����˵Ľ������ƶ� | D�� | ֻ���������ֵļ���С |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ���� | B�� | ��С | C�� | ���� | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
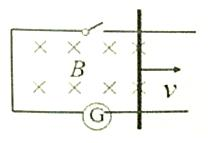 ��ͼ��ʾ���ڴŸ�Ӧǿ��ΪB��������ͼ��ʾ����ǿ�ų��У�һ���п��ص��߿�����һ�����������������ٶ�v���������˶�����Ȧ����һ�����������ز��պ�ʱ����Ȧ�������Ӧ������
��ͼ��ʾ���ڴŸ�Ӧǿ��ΪB��������ͼ��ʾ����ǿ�ų��У�һ���п��ص��߿�����һ�����������������ٶ�v���������˶�����Ȧ����һ�����������ز��պ�ʱ����Ȧ�������Ӧ�������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ��ʾ�����������ǿ�糡������ֱ���£���ǿ�ų���ֱֽ��������е���ͬ�ֵ�ɵ�����Һ���ڴ˿ռ��У�aҺ�ξ�ֹ������bҺ����ˮƽ��������ֱ���˶���cҺ����ˮƽ��������ֱ���˶���������˵������ȷ���ǣ�������
��ͼ��ʾ�����������ǿ�糡������ֱ���£���ǿ�ų���ֱֽ��������е���ͬ�ֵ�ɵ�����Һ���ڴ˿ռ��У�aҺ�ξ�ֹ������bҺ����ˮƽ��������ֱ���˶���cҺ����ˮƽ��������ֱ���˶���������˵������ȷ���ǣ�������| A�� | ����Һ�ζ������� | |
| B�� | Һ��b������һ������Һ��c������ | |
| C�� | ����Һ����Һ��c������� | |
| D�� | Һ��b��Һ��cһ������������ֱ���˶� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �����ǵĵ�һ�����ٶ�Ϊ$\frac{��R}{T}$ | |
| B�� | ����ɴ��Ƹ�������Բ���˶������ڲ����ڦ�t$\sqrt{\frac{2R}{h}}$ | |
| C�� | �����ǵ�ƽ���ܶ�Ϊ$\frac{3h}{2��RG{t}^{2}}$ | |
| D�� | ��������Ǵ���һ��ͬ�����ǣ�������DZ���߶�Ϊ$\root{3}{\frac{h{T}^{2}{R}^{2}}{2{��}^{2}{t}^{2}}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �״���һȭ���Ҹе�ʹ������δ�о���ʹ��˵������ʩ������������δ�Լ�ʩ���� | |
| B�� | ���紵�ݶ��������ܵ���������û��ʩ�����壬˵��û��ʩ���������Ҳ���е� | |
| C�� | ʩ������ʩ�����ȣ��������������ں� | |
| D�� | �����˶�Ա��������������ɳ�������������ʩ�����岻���� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com