
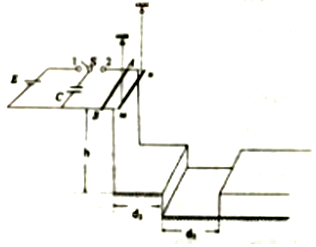
 如图所示,金属棒AB的质量m1=4.0×10-3kg,放置在宽L1=1.0m的光滑金属导轨临近边缘处,两金属导轨处于水平平面内,空间有竖直方向上的磁感应强度B=0.5T的匀强磁场,电容器的电容C,电源的电动势E,导轨平面距水平地面的高度h=0.8m,地面上距离导轨末端水平距离d1=0.6m有一个宽度也是d2=0.6m的一个深沟,在开关S与“1”接通并稳定后,再使它与“2”接通,则金属棒ab适当加速后运动到轨道末端刚好与用不可伸长的轻质软绳悬挂的金属棒MN发生弹性碰撞,碰撞前后两个金属棒的速度均为水平方向,已知金属棒MN的质量m2=1.0×10-3kg,轻质软绳长度为L2=0.4m,碰后金属棒AB做平抛运动,若悬挂金属棒MN的轻质软绳始终不松弛,并且保证金属棒AB落入深沟中.不计一切阻力,重力加速度g=10m/s2(电容C,电动势E未知,计算结果保留两位有效数字)
如图所示,金属棒AB的质量m1=4.0×10-3kg,放置在宽L1=1.0m的光滑金属导轨临近边缘处,两金属导轨处于水平平面内,空间有竖直方向上的磁感应强度B=0.5T的匀强磁场,电容器的电容C,电源的电动势E,导轨平面距水平地面的高度h=0.8m,地面上距离导轨末端水平距离d1=0.6m有一个宽度也是d2=0.6m的一个深沟,在开关S与“1”接通并稳定后,再使它与“2”接通,则金属棒ab适当加速后运动到轨道末端刚好与用不可伸长的轻质软绳悬挂的金属棒MN发生弹性碰撞,碰撞前后两个金属棒的速度均为水平方向,已知金属棒MN的质量m2=1.0×10-3kg,轻质软绳长度为L2=0.4m,碰后金属棒AB做平抛运动,若悬挂金属棒MN的轻质软绳始终不松弛,并且保证金属棒AB落入深沟中.不计一切阻力,重力加速度g=10m/s2(电容C,电动势E未知,计算结果保留两位有效数字)分析 (1)根据左手定则判断磁场的方向.
(2)对电容器通过AB棒放电的过程,运用动量定理列式.AB棒和MN棒发生弹性碰撞,根据动量守恒定律和动能守恒列式.若悬挂MN棒的软绳不松弛,有两种情况:MN棒摆动的最大高度不大于L2.第二种情况,MN棒能在竖直面内做圆周运动并能通过最高点.结合临界条件和平抛运动的规律求解.
解答 解:(1)开关接在2时,通过AB棒的电流从A到B,AB棒所受的安培力向右,由左手定则判断可知磁场方向竖直向下
(2)开关接在2时,对AB棒,由动量定理有:
$B\overline I{L_1}△t={m_1}v$,$q=\overline I△t$
AB棒和MN棒发生弹性碰撞,设碰后AB棒的速度为v1,MN棒的速度为v2,取向右为正方向,则由动量守恒定律和动能守恒得:
m1v=m1v1+m2v2
$\frac{1}{2}{m_1}{v^2}=\frac{1}{2}{m_1}v_1^2+\frac{1}{2}{m_2}v_2^2$
若悬挂MN棒的软绳不松弛,有两种情况:
第一种情况:MN棒摆动的最大高度为h1:
由动能定理得:$-{m_2}g{h_1}=0-\frac{1}{2}{m_2}v_2^2$,h1≤L2
解得:${v_2}≤2\sqrt{2}m/s$
第二种情况,MN棒能在竖直面内做圆周运动并能通过最高点,设其通过最高点的速度为vx,软绳的拉力为F0,则有:
${F_0}+{m_2}g={m_2}\frac{v_x^2}{L_2}$,且F0≥0
由动能定理得 $-{m_2}g(2{L_2})=\frac{1}{2}{m_2}v_x^2-\frac{1}{2}{m_2}v_2^2$,解得 ${v_2}≥2\sqrt{5}m/s$
保证AB棒平抛后掉入深沟里,则:
$h=\frac{1}{2}g{t^2}$,x=v1t
由几何关系有 d1≤x≤d1+d2
解得 1.5m/s≤v1≤3.0m/s
联立③④当${v_2}≤2\sqrt{2}m/s$时,${v_1}≤\frac{{3\sqrt{2}}}{4}m/s≈1.06m/s<1.5m/s$,故MN棒的第一种情况不成立,舍去.
联立③④当${v_2}≥2\sqrt{5}m/s$时,${v_1}≥\frac{{3\sqrt{5}}}{4}m/s≈1.67m/s>1.5m/s$,故MN棒的第二种情况成立.
综上所述:$\frac{{3\sqrt{5}}}{4}m/s≤{v_1}≤3.0m/s$,故$\frac{{5\sqrt{5}}}{4}m/s≤v≤5.0m/s$
再由①②解得 2.2×10-2C≤q≤4.0×10-2C.
答:
(1)磁场方向竖直向下.
(2)电容器减少的电荷量范围为:2.2×10-2C≤q≤4.0×10-2C.
点评 本题中电容器通过金属棒放电过程,往往运用动量定理求电荷量.要分析清楚两棒的运动过程,把握隐含的临界条件,注意不能漏解.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中物理 来源: 题型:计算题
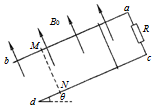 如图所示,ab、cd为间距d=1m的光滑倾斜金属导轨,与水平面的夹角θ=37°,导轨电阻不计,a、c间连接电阻R=2.4Ω.空间存在磁感应强度B0=2T的匀强磁场,方向垂直于导轨平面向上.将一根金属棒放置在导轨上距ac为x0=0.5m处,其质量m=0.5kg,电阻r=0.8Ω.现将金属棒由静止释放,金属棒沿导轨向下运动过程中始终与ac平行且与导轨接触良好.已知当金属棒从初始位置向下滑行x=1.6m到达MN处时已经达到稳定速度,金属导轨足够长,sin37°=0.6,cos37°=0.8,g取10m/s2.求:
如图所示,ab、cd为间距d=1m的光滑倾斜金属导轨,与水平面的夹角θ=37°,导轨电阻不计,a、c间连接电阻R=2.4Ω.空间存在磁感应强度B0=2T的匀强磁场,方向垂直于导轨平面向上.将一根金属棒放置在导轨上距ac为x0=0.5m处,其质量m=0.5kg,电阻r=0.8Ω.现将金属棒由静止释放,金属棒沿导轨向下运动过程中始终与ac平行且与导轨接触良好.已知当金属棒从初始位置向下滑行x=1.6m到达MN处时已经达到稳定速度,金属导轨足够长,sin37°=0.6,cos37°=0.8,g取10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
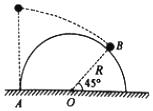 如图所示,一小球从一半圆轨道左端A点正上方某处开始做平抛运动(小球可视为质点),飞行过程中恰好与半圆轨道相切于B点.O为半圆轨道圆心,半圆轨道半径为R,OB与水平方向夹角为45°,重力加速度为g,则小球抛出时的初速度为( )
如图所示,一小球从一半圆轨道左端A点正上方某处开始做平抛运动(小球可视为质点),飞行过程中恰好与半圆轨道相切于B点.O为半圆轨道圆心,半圆轨道半径为R,OB与水平方向夹角为45°,重力加速度为g,则小球抛出时的初速度为( )| A. | $\sqrt{\frac{\sqrt{2}}{2}gR}$ | B. | $\sqrt{(\frac{\sqrt{2}}{2}+1)gR}$ | C. | $\sqrt{(1-\frac{\sqrt{2}}{2})gR}$ | D. | $\sqrt{(\sqrt{2}-1)gR}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 某人乘电梯下楼,在竖直下降的过程中,电梯速度的平方v2与下降的位移x的关系如图所示,则人对地板的压力( )
某人乘电梯下楼,在竖直下降的过程中,电梯速度的平方v2与下降的位移x的关系如图所示,则人对地板的压力( )| A. | x=1m时大于人的重力 | B. | x=11m时大于人的重力 | ||
| C. | x=21m时大于人的重力 | D. | x=21m时等于人的重力 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
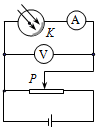 如图所示的光电管实验中,当用波长3.0×10-7m的光照射在阴极K上时,电流表有示数.调节滑动变阻器,当电压表读数为3.0V时,电流表读数恰好为零;改用波长为1.5×10-7m的光照射在阴极K上时,调节滑动变阻器,当电压表读数为7.1V时,电流表读数也恰好为零.由此可得普朗克常量为6.6×10-34J•s,该阴极的逸出功为1.8×10-19J.已知电子电量为1.6×10-19C,光速c为3×108m/s,结果保留两位有效数字.
如图所示的光电管实验中,当用波长3.0×10-7m的光照射在阴极K上时,电流表有示数.调节滑动变阻器,当电压表读数为3.0V时,电流表读数恰好为零;改用波长为1.5×10-7m的光照射在阴极K上时,调节滑动变阻器,当电压表读数为7.1V时,电流表读数也恰好为零.由此可得普朗克常量为6.6×10-34J•s,该阴极的逸出功为1.8×10-19J.已知电子电量为1.6×10-19C,光速c为3×108m/s,结果保留两位有效数字.查看答案和解析>>
科目:高中物理 来源: 题型:实验题
 如图(a)所示,是某学习小组用打点计时器验证动量守恒定律的实验装置,在气垫导轨上悬浮停放甲、乙两滑块,甲滑块连接一穿过打点计时器的纸带.当甲滑块受到水平向右的瞬时冲量后,随即启动打点计时器,甲滑块运动一段距离后,与静止的乙滑块正碰并粘合成一体继续运动,纸带记录下碰撞前甲滑块和碰撞后两滑块运动情况如图(b)所示.已测得甲滑块的质量m甲=0.40kg,乙滑块的质量m乙=0.18kg,电源频率为50Hz.由测量结果可得:
如图(a)所示,是某学习小组用打点计时器验证动量守恒定律的实验装置,在气垫导轨上悬浮停放甲、乙两滑块,甲滑块连接一穿过打点计时器的纸带.当甲滑块受到水平向右的瞬时冲量后,随即启动打点计时器,甲滑块运动一段距离后,与静止的乙滑块正碰并粘合成一体继续运动,纸带记录下碰撞前甲滑块和碰撞后两滑块运动情况如图(b)所示.已测得甲滑块的质量m甲=0.40kg,乙滑块的质量m乙=0.18kg,电源频率为50Hz.由测量结果可得:查看答案和解析>>
科目:高中物理 来源: 题型:实验题
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
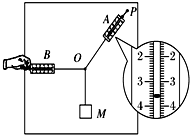 某同学用如图所示的实验装置来验证“力的平行四边形定则”,弹簧测力计A挂于固定点P,下端用细线挂一重物M,弹簧测力计B的一端用细线系于O点,手持另一端向左拉,使结点O静止在某位置,分别读出弹簧测力计A和B的示数,并在贴于竖直木板的白纸上记录O点的位置和拉线的方向
某同学用如图所示的实验装置来验证“力的平行四边形定则”,弹簧测力计A挂于固定点P,下端用细线挂一重物M,弹簧测力计B的一端用细线系于O点,手持另一端向左拉,使结点O静止在某位置,分别读出弹簧测力计A和B的示数,并在贴于竖直木板的白纸上记录O点的位置和拉线的方向查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com