
分析 根据人造卫星的万有引力等于向心力,列式求出线速度、周期的表达式进行讨论即可.
解答 解:根据万有引力提供向心力为:
$G\frac{Mm}{{r}^{2}}=m\frac{4{π}^{2}r}{{T}^{2}}=m\frac{{v}^{2}}{r}$=mω2r,
解得:v=$\sqrt{\frac{GM}{r}}$,$ω=\sqrt{\frac{GM}{{r}^{3}}}$,T=$\sqrt{\frac{4{π}^{2}{r}^{3}}{GM}}$,
则r越大,v越小,ω越小,T越大.
故答案为:①v=$\sqrt{\frac{GM}{r}}$;越小;②$ω=\sqrt{\frac{GM}{{r}^{3}}}$;越小;③T=$\sqrt{\frac{4{π}^{2}{r}^{3}}{GM}}$;越大
点评 解决本题的关键掌握万有引力提供向心力这一重要理论,知道线速度、角速度、周期、向心加速度与轨道半径的关系.


科目:高中物理 来源: 题型:解答题
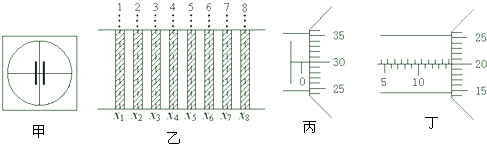
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
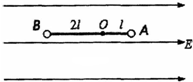 如图,在电场强度为E、方向水平向右的匀强电场中,有两个质量均为m的小球A、B(可被视为质点),被固定在一根绝缘轻杆的两端,轻杆可绕与电场方向垂直的固定转动轴O无摩擦转动,小球A、B与轴O间的距离分别为l、2l,小球A,B带电量均为+q.已知$\frac{Eq}{mg}$=$\frac{1}{2}$,重力加速度为g,静电力常量为k.从图示位置,用外力使轻杆绕O缓慢转动180°,求:
如图,在电场强度为E、方向水平向右的匀强电场中,有两个质量均为m的小球A、B(可被视为质点),被固定在一根绝缘轻杆的两端,轻杆可绕与电场方向垂直的固定转动轴O无摩擦转动,小球A、B与轴O间的距离分别为l、2l,小球A,B带电量均为+q.已知$\frac{Eq}{mg}$=$\frac{1}{2}$,重力加速度为g,静电力常量为k.从图示位置,用外力使轻杆绕O缓慢转动180°,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 均匀变化的磁场能够在空间产生均匀变化的电场 | |
| B. | 电磁波在真空和介质中传播速度相同 | |
| C. | 只要有电场和磁场就能产生电磁波 | |
| D. | 电磁波的传播不依赖于介质,在真空中也能传播 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
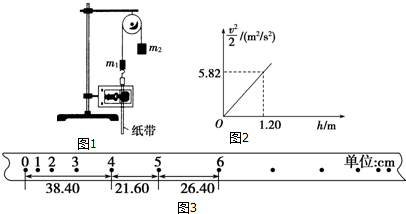
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 振子在振动过程中,速度相同时,弹簧的长度一定相等 | |
| B. | 振子从最低点向平衡位置运动过程中,弹簧弹力始终做负功 | |
| C. | 振子在运动过程中的回复力由弹簧的弹力提供 | |
| D. | 振子在运动过程中,系统的机械能守恒 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
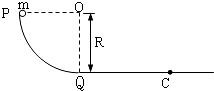 PQ是竖直平面内的$\frac{1}{4}$圆弧轨道,其下端Q与水平直轨道相切,如图所示.一小球自P点起由静止开始沿轨道下滑.已知圆轨道半径为3m,小球的质量为1kg,不计各处摩擦(g取10m/s2).求:
PQ是竖直平面内的$\frac{1}{4}$圆弧轨道,其下端Q与水平直轨道相切,如图所示.一小球自P点起由静止开始沿轨道下滑.已知圆轨道半径为3m,小球的质量为1kg,不计各处摩擦(g取10m/s2).求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
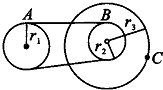 如图所示的皮带传动装置中,右边两轮连在一起同轴转动,图中三轮半径的关系为:r1=2r2,r3=1.5r1,A、B、C三点为三个轮边缘上的点,皮带不打滑.求:
如图所示的皮带传动装置中,右边两轮连在一起同轴转动,图中三轮半径的关系为:r1=2r2,r3=1.5r1,A、B、C三点为三个轮边缘上的点,皮带不打滑.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com