
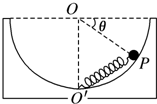
 如图所示,将一劲度系数为k的轻弹簧一端固定在内壁光滑的半球形容器底部O′处(O为球心),弹簧另一端与质量为m的小球相连,小球静止于P点.已知容器半径为R,与水平面间的动摩擦因数为μ,OP与水平方向的夹角为θ=30°.下列说法正确的是( )
如图所示,将一劲度系数为k的轻弹簧一端固定在内壁光滑的半球形容器底部O′处(O为球心),弹簧另一端与质量为m的小球相连,小球静止于P点.已知容器半径为R,与水平面间的动摩擦因数为μ,OP与水平方向的夹角为θ=30°.下列说法正确的是( )| A. | 容器相对于水平面有向左运动的趋势 | |
| B. | 容器对小球的作用力指向球心O | |
| C. | 轻弹簧对小球的作用力大小为$\frac{\sqrt{3}}{2}$mg | |
| D. | 弹簧原长为R+$\frac{mg}{k}$ |
分析 对容器和小球整体研究,分析受力可求得半球形容器受到的摩擦力.
对小球进行受力分析可知,小球受重力、支持力及弹簧的弹力而处于静止,由共点力的平衡条件可求得小球受到的轻弹簧的弹力及小球受到的支持力,由胡克定律求出弹簧的压缩量,即可求得原长.
解答 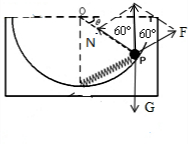 解:A、由于容器和小球组成的系统处于平衡状态,容器相对于水平面没有向左运动的趋势,故A错误;
解:A、由于容器和小球组成的系统处于平衡状态,容器相对于水平面没有向左运动的趋势,故A错误;
B、容器对小球的作用力是弹力,指向球心O,故B正确;
C、对小球受力分析,如图所示,由θ=30°可知,支持力和弹簧的弹力之间的夹角为120°,则由几何关系可知,小球受到容器的支持力和弹簧对小球的弹力大小均为mg,故C错误;
D、图中弹簧长度为R,压缩量为$\frac{mg}{k}$,故原长为R+$\frac{mg}{k}$,故D正确.
故选:BD.
点评 本题考查共点力的平衡条件应用,要注意明确共点力平衡问题重点在于正确选择研究对象,本题运用隔离法和整体法两种方法进行受力分析得出结论.同时注意几何关系的正确应用.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中物理 来源: 题型:解答题
 如图,人重600N,木块A重400N,人与A、A与地面间的动摩擦因数均为0.2,现人用水平拉绳,使他与木块一起向右匀速直线运动,滑轮摩擦不计,求:
如图,人重600N,木块A重400N,人与A、A与地面间的动摩擦因数均为0.2,现人用水平拉绳,使他与木块一起向右匀速直线运动,滑轮摩擦不计,求:查看答案和解析>>
科目:高中物理 来源: 题型:填空题
 图是霓虹灯的供电电路图,变压器可视为理想变压器.已知变压器原线圈与副线圈匝数比$\frac{{n}_{1}}{{n}_{2}}$=$\frac{1}{20}$,加在原线圈的电压为u1=311sin 100πt(V).霓虹灯正常工作的电阻R=440kΩ,则副线圈两端电压为4400V,副线圈中的电流为10.0mA.
图是霓虹灯的供电电路图,变压器可视为理想变压器.已知变压器原线圈与副线圈匝数比$\frac{{n}_{1}}{{n}_{2}}$=$\frac{1}{20}$,加在原线圈的电压为u1=311sin 100πt(V).霓虹灯正常工作的电阻R=440kΩ,则副线圈两端电压为4400V,副线圈中的电流为10.0mA.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 转笔是一项深受广大学生喜爱的休闲活动,如图所示,长为L的笔绕笔杆上的O点做圆周运动,当笔尖的速度为v1时,笔帽的速度为v2,则转轴O到笔尖的距离为( )
转笔是一项深受广大学生喜爱的休闲活动,如图所示,长为L的笔绕笔杆上的O点做圆周运动,当笔尖的速度为v1时,笔帽的速度为v2,则转轴O到笔尖的距离为( )| A. | $\frac{({v}_{1}+{v}_{2})L}{{v}_{2}}$ | B. | $\frac{({v}_{1}+{v}_{2})L}{{v}_{1}}$ | C. | $\frac{{v}_{1}L}{({v}_{1}+{v}_{2})}$ | D. | $\frac{{v}_{2}L}{({v}_{1}+{v}_{2})}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图甲所示,轻杆一端固定在O点,另一端固定一小球,现让小球在竖直平面内做半径为R的圆周运动.小球运动到最高点时,杆与小球间弹力大小为F,小球在最高点的速度大小为v,其F-v2图象如,乙图所示.则( )
如图甲所示,轻杆一端固定在O点,另一端固定一小球,现让小球在竖直平面内做半径为R的圆周运动.小球运动到最高点时,杆与小球间弹力大小为F,小球在最高点的速度大小为v,其F-v2图象如,乙图所示.则( )| A. | 小球的质量为$\frac{aR}{b}$ | B. | 当地的重力加速度小为$\frac{R}{b}$ | ||
| C. | v2=c时,杆对小球弹力方向向上 | D. | v2=b时,杆对小球弹力大小为2mg |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
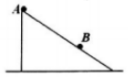 如图所示是一固定光滑斜面,A物体从斜面顶端由静止开始下滑,当A物体下滑L距离时,B物体开始从离斜面顶端距离为2L的位置由静止开始下滑,最终A、B两物体同时到达斜面底端,则该斜面的总长度为( )
如图所示是一固定光滑斜面,A物体从斜面顶端由静止开始下滑,当A物体下滑L距离时,B物体开始从离斜面顶端距离为2L的位置由静止开始下滑,最终A、B两物体同时到达斜面底端,则该斜面的总长度为( )| A. | $\frac{9L}{4}$ | B. | $\frac{17L}{8}$ | C. | 3L | D. | 4L |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 一只蜘蛛在竖直墙角处拉了一根丝线,如图所示,丝线的两个结点A,B距墙角O均为1m,现蜘蛛在距O点0.8m的P点以一定的水平初速度v0向丝线跃去,其运动可视为平抛运动,抓住丝线后,沿丝线爬到B点,g=10m/s2,则下列说法正确的是( )
一只蜘蛛在竖直墙角处拉了一根丝线,如图所示,丝线的两个结点A,B距墙角O均为1m,现蜘蛛在距O点0.8m的P点以一定的水平初速度v0向丝线跃去,其运动可视为平抛运动,抓住丝线后,沿丝线爬到B点,g=10m/s2,则下列说法正确的是( )| A. | 初速度v0的最小值为1m/s | |
| B. | 初速度v0的最小值为2m/s | |
| C. | 蜘蛛从跃出到抓住丝线最短用时为0.1s | |
| D. | 蜘蛛从跃出到抓住丝线最短用时为0.2s |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com