
 [cos(α+β)+cos(α-β)]}( )
[cos(α+β)+cos(α-β)]}( )
科目:高中物理 来源: 题型:
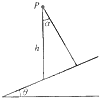 如图所示,一质点位于倾角为θ的斜面上方P点,距斜面的竖直距离为h,该质点自静止无摩檫地沿一与竖直方向夹角为α的斜槽滑至斜面上,为使质点在最短时间内从P点到达斜面,则斜面与竖直方向的夹角α应为:{积化和差公式:cosαcosβ=
如图所示,一质点位于倾角为θ的斜面上方P点,距斜面的竖直距离为h,该质点自静止无摩檫地沿一与竖直方向夹角为α的斜槽滑至斜面上,为使质点在最短时间内从P点到达斜面,则斜面与竖直方向的夹角α应为:{积化和差公式:cosαcosβ=| 1 |
| 2 |
查看答案和解析>>
科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源: 题型:单选题
 如图所示,一质点位于倾角为θ的斜面上方P点,距斜面的竖直距离为h,该质点自静止无摩檫地沿一与竖直方向夹角为α的斜槽滑至斜面上,为使质点在最短时间内从P点到达斜面,则斜面与竖直方向的夹角α应为:{积化和差公式cosαcosβ=
如图所示,一质点位于倾角为θ的斜面上方P点,距斜面的竖直距离为h,该质点自静止无摩檫地沿一与竖直方向夹角为α的斜槽滑至斜面上,为使质点在最短时间内从P点到达斜面,则斜面与竖直方向的夹角α应为:{积化和差公式cosαcosβ= [cos(α+β)+cos(α-β)]}
[cos(α+β)+cos(α-β)]}查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com