
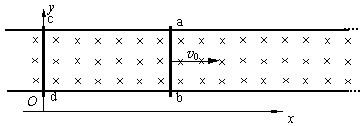
(25分)如图所示,有二平行金属导轨,相距l,位于同一水平面内(图中纸面),处在磁感应强度为B的匀强磁场中,磁场方向竖直向下(垂直纸面向里).质量均为m的两金属杆ab和cd放在导轨上,与导轨垂直.初始时刻, 金属杆ab和cd分别位于x = x0和x = 0处.假设导轨及金属杆的电阻都为零,由两金属杆与导轨构成的回路的自感系数为L.今对金属杆ab施以沿导轨向右的瞬时冲量,使它获得初速![]() .设导轨足够长,
.设导轨足够长,![]() 也足够大,在运动过程中,两金属杆之间距离的变化远小于两金属杆的初始间距
也足够大,在运动过程中,两金属杆之间距离的变化远小于两金属杆的初始间距![]() ,因而可以认为在杆运动过程中由两金属杆与导轨构成的回路的自感系数L是恒定不变的.杆与导轨之间摩擦可不计.求任意时刻两杆的位置xab和xcd以及由两杆和导轨构成的回路中的电流i三者各自随时间t的变化关系.
,因而可以认为在杆运动过程中由两金属杆与导轨构成的回路的自感系数L是恒定不变的.杆与导轨之间摩擦可不计.求任意时刻两杆的位置xab和xcd以及由两杆和导轨构成的回路中的电流i三者各自随时间t的变化关系.
解法Ⅰ:
当金属杆ab获得沿x轴正方向的初速v0时,因切割磁力线而产生感应电动势,由两金属杆与导轨构成的回路中会出现感应电流.由于回路具有自感系数,感应电流的出现,又会在回路中产生自感电动势,自感电动势将阻碍电流的增大,所以,虽然回路的电阻为零,但回路的电流并不会趋向无限大,当回路中一旦有了电流,磁场作用于杆ab的安培力将使ab杆减速,作用于cd杆的安培力使cd杆运动.
设在任意时刻t,ab杆和cd杆的速度分别为v1和v2(相对地面参考系S),当v1、v2为正时,表示速度沿x轴正方向;若规定逆时针方向为回路中电流和电动势的正方向,则因两杆作切割磁力线的运动而产生的感应电动势
![]() (1)
(1)
当回路中的电流i随时间的变化率为![]() 时,回路中的自感电动势
时,回路中的自感电动势
![]() (2)
(2)
根据欧姆定律,注意到回路没有电阻,有
![]() (3)
(3)
金属杆在导轨上运动过程中,两杆构成的系统受到的水平方向的合外力为零,系统的质心作匀速直线运动.设系统质心的速度为VC,有
![]() (4)
(4)
得
![]() (5)
(5)
VC方向与v0相同,沿x轴的正方向.
现取一新的参考系![]() ,它与质心固连在一起,并把质心作为坐标原点
,它与质心固连在一起,并把质心作为坐标原点![]() ,取坐标轴
,取坐标轴![]() 与x轴平行.设相对
与x轴平行.设相对![]() 系,金属杆ab的速度为u,cd杆的速度为
系,金属杆ab的速度为u,cd杆的速度为![]() ,则有
,则有
![]() (6)
(6)
![]() (7)
(7)
因相对![]() 系,两杆的总动量为零,即有
系,两杆的总动量为零,即有
![]() (8)
(8)
由(1)、(2)、(3)、(5)、(6) 、(7) 、(8)各式,得
![]() (9)
(9)
在![]() 系中,在t时刻,金属杆ab坐标为
系中,在t时刻,金属杆ab坐标为![]() ,在t+Δt时刻,它的坐标为
,在t+Δt时刻,它的坐标为![]() ,则由速度的定义
,则由速度的定义
![]() (10)
(10)
代入 (9) 式得
![]() (11)
(11)
若将![]() 视为i的函数,由(11)式知
视为i的函数,由(11)式知![]() 为常数,所以
为常数,所以![]() 与i的关系可用一直线方程表示
与i的关系可用一直线方程表示
![]() (12)
(12)
式中b为常数,其值待定.现已知在t=0时刻,金属杆ab在![]() 系中的坐标
系中的坐标![]() =
=![]() ,这时i = 0,故得
,这时i = 0,故得
![]() (13)
(13)
或 ![]() (14)
(14)
![]() 表示t=0时刻金属杆ab的位置.
表示t=0时刻金属杆ab的位置.![]() 表示在任意时刻t,杆ab的位置,故
表示在任意时刻t,杆ab的位置,故![]() 就是杆ab在t时刻相对初始位置的位移,用X表示,
就是杆ab在t时刻相对初始位置的位移,用X表示,
![]() (15)
(15)
当X>0时,ab杆位于其初始位置的右侧;当X<0时,ab杆位于其初始位置的左侧.代入(14)式,得
![]() (16)
(16)
这时作用于ab杆的安培力
![]() (17)
(17)
ab杆在初始位置右侧时,安培力的方向指向左侧;ab杆在初始位置左侧时,安培力的方向指向右侧,可知该安培力具有弹性力的性质.金属杆ab的运动是简谐振动,振动的周期
![]() (18)
(18)
在任意时刻t, ab杆离开其初始位置的位移
![]() (19)
(19)
A为简谐振动的振幅,φ 为初相位,都是待定的常量.通过参考圆可求得ab杆的振动速度
![]() (20)
(20)
(19)、(20)式分别表示任意时刻ab杆离开初始位置的位移和运动速度.现已知在t=0时刻,ab杆位于初始位置,即
X = 0
速度
![]()
故有
![]()
![]()
解这两式,并注意到(18)式得
![]() (21)
(21)
![]() (22)
(22)
由此得ab杆的位移
![]() (23)
(23)
由 (15) 式可求得ab杆在![]() 系中的位置
系中的位置
![]() (24)
(24)
因相对质心,任意时刻ab杆和cd杆都在质心两侧,到质心的距离相等,故在![]() 系中,cd杆的位置
系中,cd杆的位置
![]() (25)
(25)
相对地面参考系S,质心以![]() 的速度向右运动,并注意到(18)式,得ab杆在地面参考系中的位置
的速度向右运动,并注意到(18)式,得ab杆在地面参考系中的位置
![]() (26)
(26)
cd杆在S系中的位置
![]() (27)
(27)
回路中的电流由 (16) 式得
![]() (28)
(28)
解法Ⅱ:
当金属杆在磁场中运动时,因切割磁力线而产生感应电动势,回路中出现电流时,两金属杆都要受到安培力的作用,安培力使ab杆的速度改变,使cd杆运动.设任意时刻t,两杆的速度分别为v1和v2(相对地面参考系S),若规定逆时针方向为回路电动势和电流的正方向,则由两金属杆与导轨构成的回路中,因杆在磁场中运动而出现的感应电动势为
![]() (1’)
(1’)
令u表示ab杆相对于cd杆的速度,有
![]() (2’)
(2’)
当回路中的电流i变化时,回路中有自感电动势EL,其大小与电流的变化率成正比,即有
![]() (3’)
(3’)
根据欧姆定律,注意到回路没有电阻,有
![]()
由式(2’)、(3’)两式得
![]() (4’)
(4’)
设在t时刻,金属杆ab相对于cd杆的距离为![]() ,在t+Δt时刻,ab相对于cd杆的距离为
,在t+Δt时刻,ab相对于cd杆的距离为![]() +
+![]() ,则由速度的定义,有
,则由速度的定义,有
![]() (5’)
(5’)
代入 (![]() ) 式得
) 式得
![]() (6’)
(6’)
若将![]() 视为i的函数,由(6’)式可知,
视为i的函数,由(6’)式可知,![]() 为常量,所以
为常量,所以![]() 与i的关系可以用一直线方程表示,即
与i的关系可以用一直线方程表示,即
![]() (7’)
(7’)
式中b为常数,其值待定.现已知在t=0时刻,金属杆ab相对于cd杆的距离为![]() ,这时i = 0,故得
,这时i = 0,故得
![]() (8’)
(8’)
或 ![]() (9’)
(9’)
![]() 表示t=0时刻金属杆ab相对于cd杆的位置.
表示t=0时刻金属杆ab相对于cd杆的位置.![]() 表示在任意时刻t时ab杆相对于cd杆的位置,故
表示在任意时刻t时ab杆相对于cd杆的位置,故![]() 就是杆ab在t时刻相对于cd杆的相对位置相对于它们在t=0时刻的相对位置的位移,即从t=0到t=t时间内ab杆相对于cd杆的位移
就是杆ab在t时刻相对于cd杆的相对位置相对于它们在t=0时刻的相对位置的位移,即从t=0到t=t时间内ab杆相对于cd杆的位移
![]() (10')
(10')
于是有
![]() (11’)
(11’)
任意时刻t,ab杆和cd杆因受安培力作用而分别有加速度aab和acd,由牛顿定律有
![]() (12’)
(12’)
![]() (13’)
(13’)
两式相减并注意到(![]() )式得
)式得
![]() (14’)
(14’)
式中![]() 为金属杆ab相对于cd杆的加速度,而X是ab杆相对cd杆相对位置的位移.
为金属杆ab相对于cd杆的加速度,而X是ab杆相对cd杆相对位置的位移.![]() 是常数,表明这个相对运动是简谐振动,它的振动的周期
是常数,表明这个相对运动是简谐振动,它的振动的周期
![]() (15’)
(15’)
在任意时刻t,ab杆相对cd杆相对位置相对它们初始位置的位移
![]() (16’)
(16’)
A为简谐振动的振幅,φ 为初相位,都是待定的常量.通过参考圆可求得X随时间的变化率即速度
![]() (17’)
(17’)
现已知在t=0时刻,杆位于初始位置,即X = 0,速度![]()
故有
![]()
![]()
解这两式,并注意到(15’) 式得
![]()
![]()
由此得
![]() (18’)
(18’)
因t = 0时刻,cd杆位于x = 0 处,ab杆位于x = x0 处,两者的相对位置由x0表示;设t时刻,cd杆位于x = xcd 处,ab杆位于x = xab处,两者的相对位置由xab-xcd表示,故两杆的相对位置的位移又可表示为
X = xab-xcd-x0 (19’)
所以
![]() (20’)
(20’)
(12’)和(13’)式相加,
![]()
得
![]()
由此可知,两杆速度之和为一常数即v0,所以两杆的位置xab和xcd之和应为
xab+xcd = x0+v0t (21’)
由(20’)和(21’)式相加和相减,注意到(15’)式,得
![]() (22’)
(22’)
![]() (23’)
(23’)
由(11’)、(19’)(22’)、(23’)式得回路中电流
![]() (24’)
(24’)
评分标准:本题25分.
解法Ⅰ 求得(16)式8分,(17)、(18)、(19)三式各2分. (23)式4分,(24)、(25)二式各2分,(26)、(27)、(28)三式各1分.
解法Ⅱ的评分可参照解法Ⅰ评分标准中的相应式子给分.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:高中物理 来源:不详 题型:单选题
| 1 |
| 2 |
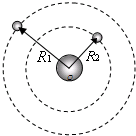
| A.加速度之比为4:1 | B.周期之比为2
| ||||
C.线速度之比为
| D.角速度之比为1:
|
查看答案和解析>>
科目:高中物理 来源:不详 题型:单选题
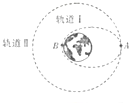
| A.卫星沿轨道Ⅰ运动,在p点的速度大于Q点的速度 |
| B.卫星沿轨道Ⅰ运动,在p点的加速度小于Q点的加速度 |
| C.卫星分别沿轨道Ⅰ、Ⅱ运动到p点的加速度不相等 |
| D.卫星要从轨道Ⅰ进人轨道Ⅱ,须在p点加速 |

查看答案和解析>>
科目:高中物理 来源:珠海二模 题型:单选题
| A.可以从较低轨道上加速 |
| B.可以从高轨道上加速 |
| C.只能从与天宫一号同一高度轨道上加速 |
| D.无论从什么轨道上,只要加速都行 |
查看答案和解析>>
科目:高中物理 来源:徐汇区一模 题型:单选题
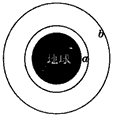
| A.v2>v1,ω2>ω1,T2<T1 | B.v2<v1,ω2>ω1,T2>T1 |
| C.v2>v1,ω2<ω1,T2>T1 | D.v2<v1,ω2<ω1,T2<T1 |
查看答案和解析>>
科目:高中物理 来源:不详 题型:填空题
查看答案和解析>>
科目:高中物理 来源:不详 题型:多选题
| A.月球的质量 | B.卫星的向心加速度 |
| C.月球对卫星的引力 | D.月球的密度 |
查看答案和解析>>
科目:高中物理 来源:不详 题型:单选题
| 公转周期 | 自转周期 | 赤道半径 | 平均密度 | |
| 地球 | 365.26天 | 23.93小时 | 6378千米 | 5.52克/厘米3 |
| 火星 | 686.98天 | 24.62小时 | 3397千米 | 3.94克/厘米3 |
| A.凤凰号进入火星表面的时速超过了地球上的第一宇宙速度 |
| B.火星到太阳的距离大于地球到太阳的距离 |
| C.用同样的速度竖直上抛一物体,(不计空气阻力)在火星上比在地球上低 |
| D.火星赤道上的线速度大于地球赤道上的线速度 |
查看答案和解析>>
科目:高中物理 来源:广东省模拟题 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com