
| A. | mg $\sqrt{2gh}$ | B. | mg$\sqrt{2gh}$cosα | C. | mg$\sqrt{2ghsinα}$ | D. | mg$\sqrt{2gh}$sinα |
科目:高中物理 来源: 题型:选择题
| A. | 人对地面的作用力大于地球对人的引力 | |
| B. | 地面对人的作用力大于人对地面的作用力 | |
| C. | 地面对人的作用力大于地球对人的引力 | |
| D. | 地面对人的作用力对人做了正功 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
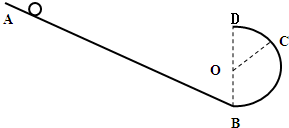 如图所示,竖直平面内的轨道由足够长的光滑斜面轨道AB和半径为R的光滑半圆形轨道BD连接而成,B为半圆形轨道的最低点,D为半圆形轨道的最高点,重力加速度为g,让质量为m的小球从斜面上某点由静止开始释放:
如图所示,竖直平面内的轨道由足够长的光滑斜面轨道AB和半径为R的光滑半圆形轨道BD连接而成,B为半圆形轨道的最低点,D为半圆形轨道的最高点,重力加速度为g,让质量为m的小球从斜面上某点由静止开始释放:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 一个弹簧振子在A、B间作简谐运动,O为平衡位置,如图甲所示,假设向右为正方向,当振子向左运动经过O点时开始计时,则图乙中画出的振动图象正确的是( )
一个弹簧振子在A、B间作简谐运动,O为平衡位置,如图甲所示,假设向右为正方向,当振子向左运动经过O点时开始计时,则图乙中画出的振动图象正确的是( )| A. |  | B. | 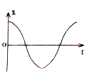 | C. | 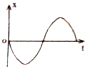 | D. |  |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 火星和木星公转周期相等 | |
| B. | 火星和木星绕太阳运行速度的大小始终相等 | |
| C. | 火星和木星公转周期之比的平方等于它们轨道半长轴之比的立方 | |
| D. | 相同时间内,火星与太阳连线扫过的面积等与木星与太阳连线扫过的面积 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
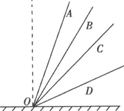 如图所示,有一系列斜面处在同一竖直面上,都位于竖直线OO′的右侧,倾角不同,它们的底端都是O点,有一些完全相同的滑块(可视为质点)从这些斜面上的A、B、C、D…各点同时由静止释放,下列判断正确的是( )
如图所示,有一系列斜面处在同一竖直面上,都位于竖直线OO′的右侧,倾角不同,它们的底端都是O点,有一些完全相同的滑块(可视为质点)从这些斜面上的A、B、C、D…各点同时由静止释放,下列判断正确的是( )| A. | 若各斜面均光滑,且这些滑块到达0点的速率相同,则A、B、C、D…各点处在同一竖直线上 | |
| B. | 若各斜面均光滑,且这些滑块到达0点所用时间相等,则A、B、C、D…各点处在同一圆周上 | |
| C. | 若各斜面与这些滑块之间的动摩擦因数相同,滑到O点的过程中,各滑块损失的机械能相同,则A、B、C、D…各点处在同一竖直线上 | |
| D. | 若各斜面与这些滑块之间的动摩擦因数相同,滑到O点的过程中,各滑块损失的机械能相同,则A、B、C、D…各点处在同一圆周上 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 一小球在外力F的作用下由A运动到B,外力F对小球做功20J,小球克服重力做功10J,克服弹力做功5J,则( )
一小球在外力F的作用下由A运动到B,外力F对小球做功20J,小球克服重力做功10J,克服弹力做功5J,则( )| A. | 小球在A点的重力势能比B点大10J | |
| B. | 小球在A点的动能比B点小5J | |
| C. | 从A点到B点过程中,小球机械能增加15J | |
| D. | 小球和弹簧组成的系统机械能守恒 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
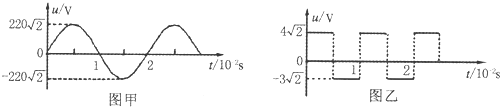
| A. | 图甲表示交流电,图乙表示直流电 | |
| B. | 图乙所示电压的有效值为5V | |
| C. | 将图甲电压通过一个理想二极管给电阻供电,电压的有效值变为110V | |
| D. | 图甲所示电压经匝数比为10:1的变压器变压后,频率变为原来的$\frac{1}{10}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题

| A. | 大小为$\frac{4{μ}_{0}ωq}{3πl}$,方向沿OO′向上 | B. | 大小为$\frac{4{μ}_{0}ωq}{3πl}$,方向沿OO′向下 | ||
| C. | 大小为$\frac{2{μ}_{0}ωq}{3πl}$,方向沿OO′向上 | D. | 大小为$\frac{2{μ}_{0}ωq}{3πl}$,方向沿OO′向下 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com