
 如图所示,电阻r=0.3Ω,质量m=0.1kg的金属棒CD垂直静置在位于水平面上的两条平行光滑金属导轨上,棒与导轨间接触良好,导轨电阻不计,导轨左端接有R=0.5Ω的电阻,有一理想电压表接在电阻R的两端,垂直导轨平面的匀强磁场向下穿过导轨平面.现给金属棒加一水平向右的恒定外力F,观察到电压表的示数逐渐变大,最后稳定在1.0V,此时导体棒的速度为2m/s.g=10m/s2.求
如图所示,电阻r=0.3Ω,质量m=0.1kg的金属棒CD垂直静置在位于水平面上的两条平行光滑金属导轨上,棒与导轨间接触良好,导轨电阻不计,导轨左端接有R=0.5Ω的电阻,有一理想电压表接在电阻R的两端,垂直导轨平面的匀强磁场向下穿过导轨平面.现给金属棒加一水平向右的恒定外力F,观察到电压表的示数逐渐变大,最后稳定在1.0V,此时导体棒的速度为2m/s.g=10m/s2.求分析 (1)根据闭合电路欧姆定律求出感应电动势,由安培力公式F=BIL求得安培力大小,由于棒匀速运动,拉力与安培力二力平衡,即可求解;
(2)根据加速度的大小,结合牛顿第二定律和安培力的表达式求出金属棒的速度,根据切割产生的电动势公式,结合欧姆定律求出电压表的示数.
(3)撤去外力F,棒在安培力作用下做减速运动,最终停止运动,由能量守恒定律即可求解
解答 解:(1)设CD杆产生的电动势为E,电流表的示数为I.
则对R研究,可知:$I=\frac{U}{R}=\frac{1}{0.5}A=2A$
棒产生的感应电动势为 E=BLv
由闭合电路欧姆定律有:$I=\frac{BLv}{R+r}$,得:$BL=\frac{{I({R+r})}}{v}=\frac{{2×({0.5+0.3})}}{2}=0.8T•m$
设CD杆受到的拉力为F,则安培力大小 FA=BIL=0.8×2N=1.6N
因为稳定时棒匀速运动,则有F=FA=1.6N,
则加速度的最大值${a_{max}}=\frac{F}{m}=16m/{s^2}$.
(2)当加速度为最大加速度一半时,a=8m/s2,
根据牛顿第二定律有:$F-\frac{{B}^{2}{L}^{2}v}{R+r}=ma$,
代入数据解得v=1m/s,
电压表的示数U=$\frac{BLv}{R+r}R=\frac{0.8×1}{0.8}×0.5$V=0.5V.
(3)由能量守恒,回路中产生的电热Q等于CD棒动能的减少量$\frac{1}{2}$mv2=Q
得:Q=$\frac{1}{2}$×0.1×22J=0.2J
电阻R上产生的电热 ${Q_R}=\frac{R}{R+r}Q=\frac{0.5}{0.5+0.3}×0.2=0.125J$.
答:(1)拉动金属棒的外力F为1.6N,此过程中金属棒的最大加速度为16m/s2;
(2)当金属棒的加速度为其最大加速度的一半时,电压表的示数为0.5V;
(3)此后电阻R上产生的热量是0.125J.
点评 本题是电磁感应与电路、力学知识的综合应用.关键掌握法拉第电磁感应定律、闭合电路欧姆定律与能量守恒定律,掌握E=BLV与F=BIL的公式的应用,同时要区别回路产生热量与电阻R的热量的区别.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中物理 来源: 题型:实验题
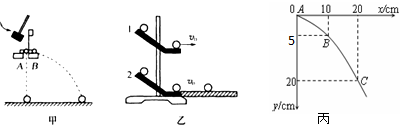
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
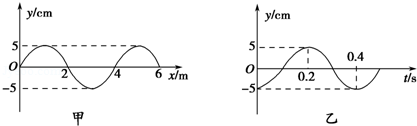
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
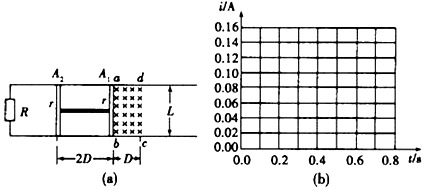 如图(a)所示,水平放置的光滑的两根平行金属导轨,间距L=0.3m.导轨左端连接R=0.6Ω的电阻,区域abcd内存在垂直于导轨平面B=0.6T的匀强磁场,磁场区域宽D=0.2m.细金属棒A1和A2用长为2D=0.4m的轻质绝缘杆连接,放置在导轨平面上,并与导轨垂直,每根金属棒在导轨间的电阻均为r=0.3Ω,导轨电阻不计,在外力作用下,使金属棒以恒定速度v=1.0m/s沿导轨向右穿越磁场,
如图(a)所示,水平放置的光滑的两根平行金属导轨,间距L=0.3m.导轨左端连接R=0.6Ω的电阻,区域abcd内存在垂直于导轨平面B=0.6T的匀强磁场,磁场区域宽D=0.2m.细金属棒A1和A2用长为2D=0.4m的轻质绝缘杆连接,放置在导轨平面上,并与导轨垂直,每根金属棒在导轨间的电阻均为r=0.3Ω,导轨电阻不计,在外力作用下,使金属棒以恒定速度v=1.0m/s沿导轨向右穿越磁场,查看答案和解析>>
科目:高中物理 来源: 题型:选择题
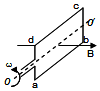 发电机线圈共N匝,每匝可简化为矩形线圈abcd,线圈在匀强磁场中绕垂直于磁场的轴OO′以角速度ω匀速转动,如图所示.此时矩形线圈ab边和cd边产生的感应电动势的最大值都为e0,不计线圈电阻,当线圈转速增加为原来的两倍时,发电机输出电压( )
发电机线圈共N匝,每匝可简化为矩形线圈abcd,线圈在匀强磁场中绕垂直于磁场的轴OO′以角速度ω匀速转动,如图所示.此时矩形线圈ab边和cd边产生的感应电动势的最大值都为e0,不计线圈电阻,当线圈转速增加为原来的两倍时,发电机输出电压( )| A. | 峰值是2e0 | B. | 峰值是4e0 | C. | 有效值是$\sqrt{2}$Ne0 | D. | 有效值是2$\sqrt{2}$Ne0 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,匀强磁场的磁感应强度B=0.5T,边长L=10cm的正方形线圈共100匝,线圈总电阻r=1Ω,线圈绕垂直于磁感线的对称轴OO'匀速转动,角速度ω=2πrad/s,外电路中的电阻R=4Ω,求:(计算结果小数点后保留两位有效数字)
如图所示,匀强磁场的磁感应强度B=0.5T,边长L=10cm的正方形线圈共100匝,线圈总电阻r=1Ω,线圈绕垂直于磁感线的对称轴OO'匀速转动,角速度ω=2πrad/s,外电路中的电阻R=4Ω,求:(计算结果小数点后保留两位有效数字)查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com