
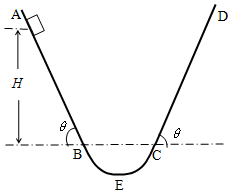
 如图所示,AB(光滑)与CD(粗糙)为两个对称斜面,斜面的倾角均为θ,其上部都足够长,下部分别与一个光滑的圆弧面BEC的两端相切,一个物体在离切点B的高度为H处,以初速度v0沿斜面向下运动,物体与CD斜面的动摩擦因数为μ.
如图所示,AB(光滑)与CD(粗糙)为两个对称斜面,斜面的倾角均为θ,其上部都足够长,下部分别与一个光滑的圆弧面BEC的两端相切,一个物体在离切点B的高度为H处,以初速度v0沿斜面向下运动,物体与CD斜面的动摩擦因数为μ.分析 (1)根据机械能守恒定律求出物体首次到达C点的速度大小;
(2)根据牛顿第二定律和速度位移公式求出物体沿斜面CD上升的最大高度h;
根据速度时间公式求出时间t;
(3)分情况讨论:①当物体与CD斜面的摩擦因数较大时,物体滑上CD斜面并匀减速上升静止在CD斜面某处;
②当物体与CD斜面的摩擦因数较小时,物体在斜面上做最大高度逐渐降低的匀变速直线运动,最终在BEC圆弧内做往复周期运动.
解答 解:(1)物体在光滑斜面AB和光滑的圆弧面BEC运动过程中,
由机械能守恒定律得,$\frac{1}{2}$mv02+mgH=$\frac{1}{2}$mvC2,
解得:vC=$\sqrt{{v}_{0}^{2}+2gH}$;
(2)由牛顿第二定律得,mgsinθ+μmgcosθ=ma,
则物体沿CD上升的加速度:a=gsinθ+μgcosθ;
由速度位移公式得,${v}_{C}^{2}$=2a$\frac{h}{sinθ}$,
解得:h=$\frac{({v}_{0}^{2}+2gH)sinθ}{2(gsinθ+μgcosθ)}$;
物体从C点上升到最高点所用的时间:
t=$\frac{{v}_{C}}{a}$=$\frac{\sqrt{{v}_{0}^{2}+2gH}}{gsinθ+μgcosθ}$;
(3)情况一:
物体滑上CD斜面并匀减速上升静止在CD斜面某处.
理由是:物体与CD斜面的摩擦因数较大.
情况二:
物体在轨道上做往复运动,在斜面上做匀变速直线运动,最大高度逐渐降低,最终在BEC圆弧内做往复周期运动.
理由是:物体在CD斜面上克服摩擦力做功机械能减少;在BEC圆弧内只有重力做功,机械能守恒.
答:(1)物体首次到达C点的速度大小为$\sqrt{{v}_{0}^{2}+2gH}$;
(2)物体沿斜面CD上升的最大高度h为$\frac{({v}_{0}^{2}+2gH)sinθ}{2(gsinθ+μgcosθ)}$;时间t为$\frac{\sqrt{{v}_{0}^{2}+2gH}}{gsinθ+μgcosθ}$;
(3)见解答.
点评 本题主要考查动能定理的应用、牛顿第二定律及匀变速直线运动公式等知识的灵活运用,关键要弄清物体在不同阶段满足的规律,熟练运用相关公式即可正确解题.


 期末集结号系列答案
期末集结号系列答案科目:高中物理 来源: 题型:计算题
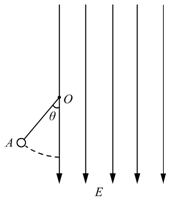 如图所示,质量m=1.0kg、带电量q=-4×10-3C的小球用长度l=0.8m的不可伸长的绝缘轻质细线悬吊在O点,过O点的竖直线右侧有竖直向下足够大的匀强电场,场强大小E=5×103N/C.现将小球拉至A处,此时,细线与竖直方向成θ角.现由静止释放小球,在小球运动过程中细线始终未被拉断.已知cosθ=$\frac{3}{4}$,取重力加速度g=10m/s2.
如图所示,质量m=1.0kg、带电量q=-4×10-3C的小球用长度l=0.8m的不可伸长的绝缘轻质细线悬吊在O点,过O点的竖直线右侧有竖直向下足够大的匀强电场,场强大小E=5×103N/C.现将小球拉至A处,此时,细线与竖直方向成θ角.现由静止释放小球,在小球运动过程中细线始终未被拉断.已知cosθ=$\frac{3}{4}$,取重力加速度g=10m/s2.查看答案和解析>>
科目:高中物理 来源: 题型:多选题
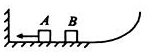 如图所示,光滑水平轨道的左边与墙壁对接,右边与一个半径为0.5m的$\frac{1}{4}$光滑竖直圆弧轨道平滑相连,物块A、B(均可视为质点)静置于光滑水平轨道上.现让物块A以6m/s的速度水平向左运动与墙壁相碰,碰撞的时间为0.01s,碰后瞬间的速度大小为5m/s.当物块A与物块B碰撞后立即粘在一起运动.已知物块A的质量为1.0kg,物块B的质量为l.5kg,g取l0m/s2.则( )
如图所示,光滑水平轨道的左边与墙壁对接,右边与一个半径为0.5m的$\frac{1}{4}$光滑竖直圆弧轨道平滑相连,物块A、B(均可视为质点)静置于光滑水平轨道上.现让物块A以6m/s的速度水平向左运动与墙壁相碰,碰撞的时间为0.01s,碰后瞬间的速度大小为5m/s.当物块A与物块B碰撞后立即粘在一起运动.已知物块A的质量为1.0kg,物块B的质量为l.5kg,g取l0m/s2.则( )| A. | 物块A、B碰撞后瞬间的速度v=2m/s | |
| B. | 物块A、B滑上圆弧轨道的最大高度h=0.05m | |
| C. | 物块A与墙壁、物块A与B碰撞过程中,系统损失的动能之比为11:15 | |
| D. | 物块A与墙壁碰撞的过程中,墙壁对A的平均作用力的大小F=100N |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 介质的折射率是$\frac{1}{\sqrt{2}}$ | |
| B. | 这束光在介质中传播的速度是1.5×108m/s | |
| C. | 这束光的频率是5×1014Hz | |
| D. | 这束光发生全反射的临界角是30° |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
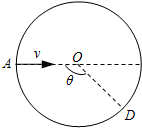 竖直平面(纸面)内有一半径为R的圆形区域,O为圆心,如图所示.在该圆形区域内加一竖直方向的匀强电场,一质量为m、电荷量为q的带正电的粒子沿图中水平直径AO从圆上的A点以速度v射入圆形区域,在圆上的D点离开该区域,已知图中θ=120°.现将电场换为充满该区域垂直纸面的匀强磁场,同一粒子以同样速度沿直径从A点射入圆形区域,也在D点离开该区域.不计粒子重力.
竖直平面(纸面)内有一半径为R的圆形区域,O为圆心,如图所示.在该圆形区域内加一竖直方向的匀强电场,一质量为m、电荷量为q的带正电的粒子沿图中水平直径AO从圆上的A点以速度v射入圆形区域,在圆上的D点离开该区域,已知图中θ=120°.现将电场换为充满该区域垂直纸面的匀强磁场,同一粒子以同样速度沿直径从A点射入圆形区域,也在D点离开该区域.不计粒子重力.查看答案和解析>>
科目:高中物理 来源: 题型:计算题
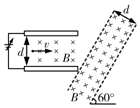 如图所示,两平行长金属板水平放置,相距为d,两极板接在电压可调的电源上.两金属板间有磁感应强度大小为B、方向垂直纸面向里的匀强磁场;金属板右侧有一宽度为d、磁感应强度大小也为B、方向垂直纸面向里的足够长匀强磁场,且磁场边界与水平方向的夹角为60°.金属板中间有一粒子发射源,能沿水平方向发射出电性不同的两种带电粒子,调节可变电源的电压,当电源电压为U时,粒子恰好能沿直线飞出金属板,粒子离开金属板进入有界磁场后分成两束,经磁场偏转后恰好同时从两边界离开磁场,且从磁场右边界离开的粒子的速度方向恰好与磁场边界垂直,粒子间的相互作用不计,粒子重力不计.求:
如图所示,两平行长金属板水平放置,相距为d,两极板接在电压可调的电源上.两金属板间有磁感应强度大小为B、方向垂直纸面向里的匀强磁场;金属板右侧有一宽度为d、磁感应强度大小也为B、方向垂直纸面向里的足够长匀强磁场,且磁场边界与水平方向的夹角为60°.金属板中间有一粒子发射源,能沿水平方向发射出电性不同的两种带电粒子,调节可变电源的电压,当电源电压为U时,粒子恰好能沿直线飞出金属板,粒子离开金属板进入有界磁场后分成两束,经磁场偏转后恰好同时从两边界离开磁场,且从磁场右边界离开的粒子的速度方向恰好与磁场边界垂直,粒子间的相互作用不计,粒子重力不计.求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 2.0×107kg/m3 | B. | 5.6×103kg/m3 | C. | 2.1×103kg/m3 | D. | 3.0×104kg/m3 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题

查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图为玻璃自动切割生产线示意图,宽L=0.9m的玻璃以恒定的速度v=0.4m/s向右运动,两侧的滑轨与玻璃的运动方向平行,滑杆与滑轨垂直,且可沿滑轨左右移动,割刀通过沿滑杆滑动和随滑杆左右移动实线对移动玻璃的切割.为了使割下的玻璃板都成规定尺寸的矩形,求:
如图为玻璃自动切割生产线示意图,宽L=0.9m的玻璃以恒定的速度v=0.4m/s向右运动,两侧的滑轨与玻璃的运动方向平行,滑杆与滑轨垂直,且可沿滑轨左右移动,割刀通过沿滑杆滑动和随滑杆左右移动实线对移动玻璃的切割.为了使割下的玻璃板都成规定尺寸的矩形,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com