
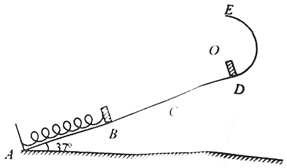
 如图所示,一轻弹簧一端同定在倾角为37°的固定光滑直轨道AD的底端AB处,另一端若自由伸长则位于C点,另一端若固定连接一质量为m的小木块,小木块处于B点时恰静止.直轨道与-半径为r=0.5R的光滑圆弧轨道相切于D点,E点为圆弧轨道的最高点(且过E点的切线水平).BC=CD=R,A、B、C、D、E均在同一竖直面内.质量为m的一小铁块自D点由静止开始下滑,到达B点后与小木块碰撞,碰撞时间极短,碰撞后共同压缩弹簧,此后运动过程中小铁块与小木块恰不分离.轻弹簧始终处于弹性限度内,重力加速度大小为g,(取sin37°=0.6.cos37°=0.8)求:
如图所示,一轻弹簧一端同定在倾角为37°的固定光滑直轨道AD的底端AB处,另一端若自由伸长则位于C点,另一端若固定连接一质量为m的小木块,小木块处于B点时恰静止.直轨道与-半径为r=0.5R的光滑圆弧轨道相切于D点,E点为圆弧轨道的最高点(且过E点的切线水平).BC=CD=R,A、B、C、D、E均在同一竖直面内.质量为m的一小铁块自D点由静止开始下滑,到达B点后与小木块碰撞,碰撞时间极短,碰撞后共同压缩弹簧,此后运动过程中小铁块与小木块恰不分离.轻弹簧始终处于弹性限度内,重力加速度大小为g,(取sin37°=0.6.cos37°=0.8)求:分析 (1)小铁块沿直轨道从D点滑到B点的过程,运用机械能守恒定律求小铁块即将与小木块碰撞时的速率.
(2)小铁块与小木块碰撞时间极短,系统的动量守恒,由动量守恒定律求出碰后共同速度.再对碰后过程,运用机械能守恒定律求小铁块即将与小木块碰撞时弹簧的弹性势能.
(3)与小木块碰撞后,要能沿着圆弧轨道运动到E点,到达E点时重力提供向心力.根据机械能守恒定律列式得到小铁块即将与小木块碰撞时的速率表达式,由动量守恒定律得到小铁块与小木块碰后的速率表达式.再对碰后小铁块与小木块分离后沿CDE轨道运动到E点的过程,由机械能守恒定律列式.在E点,根据牛顿第二定律列式,联立可解.
解答 解:(1)小铁块沿直轨道下滑时,根据机械能守恒定律有
mg•2Rsin37°=$\frac{1}{2}m{v}_{1}^{2}$
可得 v1=$\sqrt{2.4gR}$
(2)小铁块与小木块碰撞前后,由于碰撞时间极短,动量守恒,取沿斜面向下为正方向,由动量守恒定律有
mv1=2mv2.
碰后,小铁块与小木块共同压缩弹簧,直至速度减小至零后被反间向上运动,当轻弹簧恰恢复原长时,小铁块与小木块即将分离,故此时小铁块和小木块的速度均为零,根据机械能守恒定律有
$\frac{1}{2}•2m{v}_{2}^{2}$+Ep=2mgRsin37°
解得小铁块即将与小木块碰撞时弹簧的弹性势能为 Ep=0.6mgR
(3)设小铁块的初速度为v0.小铁块沿直轨道下滑时,根据机械能守恒定律有
$\frac{1}{2}m{v}_{0}^{2}$+mg•2Rsin37°=$\frac{1}{2}m{v}_{1}^{′2}$
小铁块与小木块碰撞过程,由动量守恒定律有
mv1′=2mv2′
碰后,小铁块与小木块共同压缩弹簧,直至速度减小至零后被反间向上运动,当轻弹簧恰恢复原长时,小铁块与小木块即将分离,故此时小铁块和小木块的速度均为零,根据机械能守恒定律有
$\frac{1}{2}•2m{v}_{2}^{′2}$+Ep=2mgRsin37°+$\frac{1}{2}•2m{v}_{3}^{2}$
小铁块与小木块分离后沿CDE恰好运动到E点的过程,由机械能守恒定律有
$\frac{1}{2}m{v}_{3}^{2}$=mg(Rsin37°+rcos37°+r)+$\frac{1}{2}m{v}_{E}^{2}$
在最高点E,由重力等于向心力有
mg=m$\frac{{v}_{E}^{2}}{r}$
联立解得 v0=$\sqrt{14gR}$
答:
(1)小铁块即将与小木块碰撞时的速率为$\sqrt{2.4gR}$;
(2)小铁块即将与小木块碰撞时弹簧的弹性势能为0.6mgR;
(3)小铁块的初速度至少为$\sqrt{14gR}$,与小铁块碰撞后,才能沿着圆弧轨道运动到E点.
点评 本题是多过程问题,要分析清楚铁块和木块的运动过程,灵活选择研究的过程,把握每个过程的物理规律.要知道圆周运动最高点的临界条件:重力等于向心力.


科目:高中物理 来源: 题型:选择题
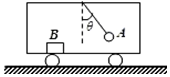 如图所示,小车运动的过程中,质量均为m的悬挂的小球A和车水平底板上的物块B都相对车厢静止,悬挂小球A的悬线与竖直线夹角为θ,则物块B受到的摩擦力和小车运动情况下列判断中正确的是( )
如图所示,小车运动的过程中,质量均为m的悬挂的小球A和车水平底板上的物块B都相对车厢静止,悬挂小球A的悬线与竖直线夹角为θ,则物块B受到的摩擦力和小车运动情况下列判断中正确的是( )| A. | 物块B不受摩擦力作用,小车只能向右运动 | |
| B. | 物块B受摩擦力作用,大小为mgtanθ,方向向左;小车可能向右运动 | |
| C. | 物块B受摩擦力作用,大小为mgtanθ,方向向左;小车一定向左运动 | |
| D. | B受到的摩擦力情况无法判断,小车运动方向不能确定 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
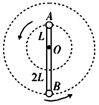 如图所示,轻杆长为3L,在杆的A、B两端分别固定质量均为m的球A和球B,杆上距球A为L处的点O装在光滑的水平转动轴上,外界给予系统一定的能量后,杆和球在竖直面内转动.在转动的过程中,忽略空气的阻力,若球B运动到最高点时,球B队杆恰好无作用力,则下列说法正确的是( )
如图所示,轻杆长为3L,在杆的A、B两端分别固定质量均为m的球A和球B,杆上距球A为L处的点O装在光滑的水平转动轴上,外界给予系统一定的能量后,杆和球在竖直面内转动.在转动的过程中,忽略空气的阻力,若球B运动到最高点时,球B队杆恰好无作用力,则下列说法正确的是( )| A. | 球B在最高点时速度为零 | |
| B. | 此时球A的速度大小为$\sqrt{\frac{gL}{2}}$ | |
| C. | 球B转到最高点时,杆对水平轴的作用力为1.5mg | |
| D. | 球B转到最高点时,杆对水平轴的作用力为3mg |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
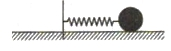 如图所示,原长为L,劲度系数为k的轻质弹簧拉着一个质量为m的小球在光滑的水平面上做匀速圆周运动.已知弹簧一直处于弹性限度内,则当弹簧的伸长量分别为L和2L时,下列说法正确的是( )
如图所示,原长为L,劲度系数为k的轻质弹簧拉着一个质量为m的小球在光滑的水平面上做匀速圆周运动.已知弹簧一直处于弹性限度内,则当弹簧的伸长量分别为L和2L时,下列说法正确的是( )| A. | 小球转动的角速度之比ω1:ω2=2:1 | |
| B. | 小球转动的线速度之比v1:v2=1:$\sqrt{3}$ | |
| C. | 小球的向心加速度之比为a1:a2=1:2 | |
| D. | 小球的周期之比为T1:T2=3:$\sqrt{3}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,小球Q在竖直平面内做匀速圆周运动,当Q球转到与O同一水平线时,有另一小球P在距圆周最高点为h处开始自由下落,要使两球在圆周最高点相碰,求:
如图所示,小球Q在竖直平面内做匀速圆周运动,当Q球转到与O同一水平线时,有另一小球P在距圆周最高点为h处开始自由下落,要使两球在圆周最高点相碰,求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
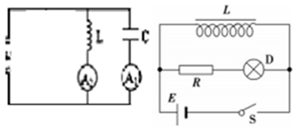 如甲图所示,交流电流表A1、A2分别与电容器C和电感线圈L串联后 接在同一个正弦式交流电源上,保持供电电压的最大值不变.如图乙图所示,电阻R和自感线圈L的电阻值都小于灯泡D的电阻,接通S,使电路达到稳定,灯泡D发光,下列说法正确的是( )
如甲图所示,交流电流表A1、A2分别与电容器C和电感线圈L串联后 接在同一个正弦式交流电源上,保持供电电压的最大值不变.如图乙图所示,电阻R和自感线圈L的电阻值都小于灯泡D的电阻,接通S,使电路达到稳定,灯泡D发光,下列说法正确的是( )| A. | 在图甲中,当供电电压的频率减少时,A1示数增大,A2示数减小 | |
| B. | 在图甲中,当供电电压的频率减小时,A1示数减小,A2示数增大 | |
| C. | 在图乙中,断开S后,D将渐渐变暗至熄灭 | |
| D. | 在图乙中,断开S后,D将变得更亮,然后渐渐变暗至熄灭 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
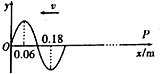 一列向左传播的简谐横波,传播速度大小为v=0.6m/s,t=1.9s时波刚传到O点,波形图如图所示,x轴上的P质点横坐标x=0.96m,则下列说法中正确的是( )
一列向左传播的简谐横波,传播速度大小为v=0.6m/s,t=1.9s时波刚传到O点,波形图如图所示,x轴上的P质点横坐标x=0.96m,则下列说法中正确的是( )| A. | 图中O质点运动方向沿y轴负方向 | |
| B. | P质点刚开始振动时运动方向沿y轴正方向 | |
| C. | P质点刚开始振动的时间为tP=0.3s | |
| D. | P质点第一次到达波谷的时间为0.6s | |
| E. | P振动的振动周期为0.3s |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com