
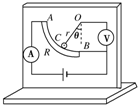
 ijͬѧ�����һ���ⶨ�г����ٶȵ���������ͼ��ʾ��AB��һ��$\frac{1}{4}$Բ���εĵ��裬O��Ϊ��Բ�ģ�Բ���뾶Ϊr��O������һ���費�ƵĽ�����������һ������������²���AB�Ӵ���������Ħ����A��B֮��������費�ơ��綯��Ϊ9V�ĵ�أ���·�н������������A��O��B�����һ�������ѹ��V������װ����һ��ֱƽ���ڣ���װ������ƽ�����г�ǰ���ķ���ƽ�У�����˵������ȷ���У�������
ijͬѧ�����һ���ⶨ�г����ٶȵ���������ͼ��ʾ��AB��һ��$\frac{1}{4}$Բ���εĵ��裬O��Ϊ��Բ�ģ�Բ���뾶Ϊr��O������һ���費�ƵĽ�����������һ������������²���AB�Ӵ���������Ħ����A��B֮��������費�ơ��綯��Ϊ9V�ĵ�أ���·�н������������A��O��B�����һ�������ѹ��V������װ����һ��ֱƽ���ڣ���װ������ƽ�����г�ǰ���ķ���ƽ�У�����˵������ȷ���У�������| A�� | ��ͼ�п����г�һ�������Ҽ����˶� | |
| B�� | ���г��ļ��ٶ�����ʱ��������A�Ķ�������ѹ��V�Ķ���Ҳ���� | |
| C�� | ����ѹ����ʾ3 V�����г��ļ��ٶ�Ϊ$\frac{\sqrt{3}}{3}$g | |
| D�� | ������ݵ�ѹ��ʾ�����г����ٶȵ�һһ��Ӧ��ϵ����ѹ�����Ƴ�һ�����ٶȱ�������ٶȱ��Ŀ̶��Ǿ��ȵ� |
���� ͨ��С��ĺ�������ȷ���г��ļ��ٶȷ������ٶ�����ʱ���жϳ��Ƚǵı仯���Ӷ���֪BC�ε���ı仯�����ݱպϵ�·ŷķ�����жϵ����͵�ѹ�ı仯��
��� �⣺A��С�����ܵĺ���ˮƽ���ң���֪�г������������˶��������������˶�����A����
B��С��ļ��ٶ�Ϊ a=gtan�ȣ������ٶ���������BC�ε���������Ϊ�ܵ��費�䣬���Ե������䣬BC�ε�ѹ����ѹ����������B����
C������ѹ��Ϊ3Vʱ��֪BC�εĵ������ܵ��������֮һ�����=30�㣬��a=gtan30��=$\frac{\sqrt{3}}{3}$g����C��ȷ��
D������a=gtan��֪��a��Ȳ������ȹ�ϵ����Ϊ�������䣬��ѹ��ʾ���Ĵ�С���������ȣ�BC�ε�����ȳ����ȣ�����a���ѹ��ʾ���Ĺ�ϵ�������ȣ����Լ��ٶȱ��Ŀ̶Ȳ����ȣ���D����
��ѡ��C
���� ���⽫�պϵ�·ŷķ������ţ�ٵڶ������ۺϣ��ؼ�֪��������ٶȵĹ�ϵ������BC�ε���Ĵ�С��ϵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ҽ����ijЩ��������ʱ�����õ��Ѫ���������ͨ��������Ѫ���ٶȣ����Ѫ������һ�Ե缫a��b�Լ��ż�N��S���ɣ��ż���Ĵų��Ǿ��ȵģ�ʹ��ʱ�����缫a��b����Ѫ�ܱڽӴ�������������ߡ��ų������Ѫ���ٶȷ���������ֱ����ͼ��ʾ������ѪҺ�е�����������Ѫ��һ���ڴų����˶����缫a��b֮�����С���Ʋ�ڴﵽƽ��ʱ��Ѫ���ڲ��ĵ糡�ɿ�������ǿ�糡��ѪҺ�е��������ܵĵ糡���ʹų����ĺ���Ϊ�㣮���й��ڵ��Ѫ���Ƶ�˵����ȷ���ǣ�������
ҽ����ijЩ��������ʱ�����õ��Ѫ���������ͨ��������Ѫ���ٶȣ����Ѫ������һ�Ե缫a��b�Լ��ż�N��S���ɣ��ż���Ĵų��Ǿ��ȵģ�ʹ��ʱ�����缫a��b����Ѫ�ܱڽӴ�������������ߡ��ų������Ѫ���ٶȷ���������ֱ����ͼ��ʾ������ѪҺ�е�����������Ѫ��һ���ڴų����˶����缫a��b֮�����С���Ʋ�ڴﵽƽ��ʱ��Ѫ���ڲ��ĵ糡�ɿ�������ǿ�糡��ѪҺ�е��������ܵĵ糡���ʹų����ĺ���Ϊ�㣮���й��ڵ��Ѫ���Ƶ�˵����ȷ���ǣ�������| A�� | a�˵��Ƹߡ�b�˵��Ƶ� | |
| B�� | a�˵��Ƶ͡�b�˵��Ƹ� | |
| C�� | ͬһ���ߣ��缫a��b֮����Ʋ�Խ��˵��Ѫ���ٶ�Խ�� | |
| D�� | ��ͬ���ߣ��缫a��b֮����Ʋͬ��Ѫ���ٶ�һ����ͬ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
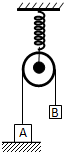 ����AB�ÿ���⻬���ֵ��������ӣ����ֹ��ڵ��ɲ������£���ͼ��ʾ����֪A��100N��B��40N��������10N��A���徲ֹ��ˮƽ�����ϣ���
����AB�ÿ���⻬���ֵ��������ӣ����ֹ��ڵ��ɲ������£���ͼ��ʾ����֪A��100N��B��40N��������10N��A���徲ֹ��ˮƽ�����ϣ����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ��A���һ������̽��ɣ�A��ij�ǿ�����Ϊˮƽ���� | |
| B�� | ��A���һ������̽��ɣ������ܵĵ糡������ˮƽ���� | |
| C�� | ��A�����һ�������Ϊ2q����̽��ɣ���A��ij�ǿ��Ϊ2EA | |
| D�� | ��A�����һ�������Ϊ2q����̽��ɣ��������ܵĵ糡����Ϊ4F |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
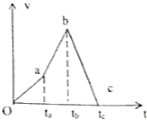
| A�� | 0��ta�λ���ļ��ٶ�С��ta��tb �λ���ļ��ٶȣ�tbʱ�̵�����ߵ� | |
| B�� | ��0��tb �λ���������ģ���tb��tc�λ��������� | |
| C�� | 0��tbʱ�̻���ڼ������� | |
| D�� | tb��tcʱ�̻���ڼ������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ����k$\frac{{Q}^{2}}{{r}^{2}}$ | B�� | С��k$\frac{{Q}^{2}}{{r}^{2}}$ | C�� | ����k$\frac{{Q}^{2}}{{r}^{2}}$ | D�� | ����ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
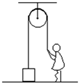 ��ͼ��ʾ��һ����200N����ͨ�����ӺͶ�������һ����ֹ�ڵ�������600N�����壬�����Ӷ����������Fr���������ܵ����֧����FN��������
��ͼ��ʾ��һ����200N����ͨ�����ӺͶ�������һ����ֹ�ڵ�������600N�����壬�����Ӷ����������Fr���������ܵ����֧����FN��������| A�� | Fr=200N��FN=400N | B�� | Fr=600N��FN=200N | C�� | Fr=200N��FN=200N | D�� | Fr=400N��FN=200N |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
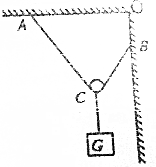 ��ͼ��ʾ����ˮƽ�컨������ֱǽ�ڼ䣬ͨ�������������������Ӻ⻬����С������������G=40N������L=2.5m��OA=1.5m�������������Ĵ�С�������ۣ�
��ͼ��ʾ����ˮƽ�컨������ֱǽ�ڼ䣬ͨ�������������������Ӻ⻬����С������������G=40N������L=2.5m��OA=1.5m�������������Ĵ�С�������ۣ��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com