
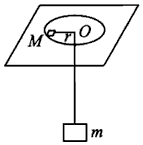
 如图,细绳一端系着质量M=0.6㎏的物体,静止在水平面,另一端通过光滑小孔吊着质量m=0.3kg的物体,M的中点与圆孔距离为0.2m,并知M和水平面的最大静摩擦力为2N,现使此平面绕中心轴线转动,问角速度ω在什么范围m会处于静止状态?(取g=9.8m/s2)
如图,细绳一端系着质量M=0.6㎏的物体,静止在水平面,另一端通过光滑小孔吊着质量m=0.3kg的物体,M的中点与圆孔距离为0.2m,并知M和水平面的最大静摩擦力为2N,现使此平面绕中心轴线转动,问角速度ω在什么范围m会处于静止状态?(取g=9.8m/s2) 分析 当M所受的最大静摩擦力沿半径方向向外时,角速度最小,当M所受的最大静摩擦力沿半径向内时,角速度最大,根据牛顿第二定律求出角速度的范围.
解答 解:当M所受的最大静摩擦力沿半径方向向外时,角速度最小,根据牛顿第二定律得,mg-Ff=Mrω12,
解得ω1=$\frac{5\sqrt{3}}{3}$rad/s
当M所受的最大静摩擦力沿半径向内时,角速度最大,mg+Ff=Mrω22,
解得ω2=$\frac{5\sqrt{15}}{3}$rad/s
答:角速度ω在$\frac{5\sqrt{3}}{3}$rad/s≤ω≤$\frac{5\sqrt{15}}{3}$rad/s范围,m会处于静止.
点评 解决本题的关键搞清圆周运动向心力的来源,抓住临界状态,运用牛顿第二定律进行求解.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
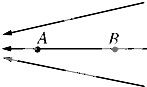
| A. | FA>FB | B. | FA<FB | ||
| C. | FA=FB | D. | 电荷正负不明,无法判断 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,两个质量相同的物体A和B,在同一高度处,A物体自由落下,B物体沿光滑斜面下滑(空气阻力不计),则( )
如图所示,两个质量相同的物体A和B,在同一高度处,A物体自由落下,B物体沿光滑斜面下滑(空气阻力不计),则( )| A. | 到达地面时速度相同,动能相同 | |
| B. | 到达地面时A物体的重力瞬时功率大 | |
| C. | A物体在运动过程中机械能守恒,B物体在运动过程中机械能不守恒 | |
| D. | B物体重力所做的功比A物体重力所做的功多 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
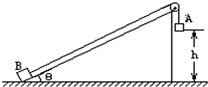 如图所示,用细绳连接的A、B两物体质量均为m,B位于倾角为30°的足够长的光滑斜面上,细绳跨过定滑轮后使A、B均保持静止,然后释放,A下降1m后落地,不计滑轮质量与摩擦,求:
如图所示,用细绳连接的A、B两物体质量均为m,B位于倾角为30°的足够长的光滑斜面上,细绳跨过定滑轮后使A、B均保持静止,然后释放,A下降1m后落地,不计滑轮质量与摩擦,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 3000m/s2 | B. | -3000m/s2 | C. | 5000m/s2 | D. | -5000m/s2 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 当r=r0时,分子势能为零 | B. | 当r=r0时,分子势能最小 | ||
| C. | 分子势能先减小后增大 | D. | 分子的势能和动能之和保持不变 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com