练习册

  • 练习册
  • 试题
    精英家教网 > 高中物理 > 题目详情
    10．两颗行星绕某恒星匀速转动，它们周期之比为27：1，则它们的轨道半径之比是（　　）
    A．1：27B．9：1C．27：1D．1：9

    分析 要求轨道半径之比，由于已知运动周期之比，故可以利用万有引力提供向心力（F向=m$\frac{{4π}^{2}}{{T}^{2}}$r）来求解．

    解答 解：行星在绕恒星做圆周运动时恒星对行星的引力提供圆周运动的向心力
    $\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}}{{T}^{2}}$r
    r=$\root{3}{\frac{G{MT}^{2}}{{4π}^{2}}}$
    它们周期之比为27：1，则它们的轨道半径之比是9：1，
    故选：B．

    点评 一个天体绕中心天体做圆周运动时万有引力提供向心力，灵活的选择向心力的表达式是我们顺利解决此类题目的基础．我们要按照不同的要求选择不同的公式来进行求解．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中物理 来源： 题型：选择题

    20．行星绕恒星的运动轨道我们近似成圆形，那么它运行的周期T的平方与轨道半径R的三次方的比例常数k，即k=$\frac{{T}^{2}}{{R}^{3}}$，则常数k的大小（　　）
    A．行星的质量有关
    B．只与恒星的质量有关
    C．与恒星的质量及行星的质量没有关系
    D．与恒星的质量及行星的质量有关系

    查看答案和解析>>

    科目：高中物理 来源： 题型：解答题

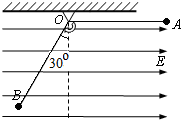    1．如图所示，在水平向右的匀强电场中，用长为L不可伸长的绝缘细线拴住一质量为m，带电荷量为q的小球，线的上端固定于O点．细线与竖直方向成30°角时静止释放小球，小球开始摆动，当摆到A点时速度为零，此时OA恰好处于水平状态，设整个过程中细线始终处于拉直状态，静电力常量为k，忽略空气阻力．
    求：（1）判断小球电性；
    （2）BA两点间的电势差UBA；
    （3）匀强电场的场强E的大小．

    查看答案和解析>>

    科目：高中物理 来源： 题型：填空题

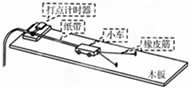    18．探究力对原来静止的物体做的功与物体获得的速度的关系，实验装置如图所示，实验主要过程如下：
    （a）设法让橡皮筋对小车做的功分别为W、2W、3W、…；
    （b）分析打出的纸带，求出小车的速度v1、v2、v3、…；
    （c）作出W-v草图；
    （d）分析W-v图象．如果W-v图象是一条直线，表明∝v；如果不是直线，可考虑是否存在W∝v2、W∝v3、W∝$\sqrt{v}$等关系．
    （1）以下关于该实验的说法中有一项不正确，它是D．
    A．本实验设法让橡皮筋对小车做的功分别为W、2W、3W、…．所采用的方法是选用同样的橡皮筋，并在每次实验中使橡皮筋拉伸的长度保持一致．当用1条橡皮筋进行实验时，橡皮筋对小车做的功为W，用2条、3条、…橡皮筋并在一起进行第2次、第3次、…实验时，橡皮筋对小车做的功分别是2W、3W、…．
    B．小车运动中会受到阻力，补偿的方法，可以使木板适当倾斜．
    C．先开打点计时器，再放纸带，得到一条记录纸带．
    D．根据纸带上打出的点，以纸带上第一点到最后一点的距离来求小车获得的速度的方法．
    （2）关于使木板适当倾斜来平衡阻力，则下面操作正确的是D．
    A．放开小车，能够自由下滑即可
    B．放开小车，能够匀速下滑即可
    C．放开拖着纸带的小车，能够自由下滑即可
    D．放开拖着纸带的小车，能够匀速下滑即可
    （3）某同学在一次实验中，纸带上打出的点，两端密、中间疏．出现这种情况的原因，最可能是最可能是没有使木板倾斜或倾角太小．

    查看答案和解析>>

    科目：高中物理 来源： 题型：多选题

    5．有关开普勒关于行星运动的描述，下列说法中正确的是（　　）
    A．所有的行星绕太阳运动的轨道都是椭圆，太阳处在椭圆的一个焦点上
    B．所有的行星绕太阳运动的轨道都是圆，太阳处在圆心上
    C．所有的行星轨道的半长轴的二次方跟公转周期的三次方的比值都相等
    D．不同的行星绕太阳运动的椭圆轨道是不同的

    查看答案和解析>>

    科目：高中物理 来源： 题型：选择题

    15．两个相同金属小球A、B均可视为点电荷，所带电荷量分别为+Q、+3Q，固定于相距为r的两点，此时A、B间库仑力的大小为F．若将小球A、B相互接触后，固定于相距为2r的另外两点，则此时A、B间库仑力的大小为（　　）
    A．$\frac{1}{12}F$B．$\frac{1}{3}F$C．$\frac{4}{3}F$D．12F

    查看答案和解析>>

    科目：高中物理 来源： 题型：选择题

    2．如图（a）所示为一列简谐横波在t=6s时的波形图，图（b）是这列波中P点的振动图线，那么该波的传播速度和传播方向是（　　）
    A．v=25 cm/s，向左传播B．v=50 cm/s，向左传播
    C．v=25 cm/s，向右传播D．v=50 cm/s，向右传播

    查看答案和解析>>

    科目：高中物理 来源： 题型：选择题

    19．据报道，“嫦娥一号”预计在2007年发射，“嫦娥一号”将在距离月球为h高处绕月球做匀速圆周运动，已知月球半径为R，月球表面的重力加速度为g0．“嫦娥一号”环绕月球运行的周期为（　　）
    A．$\frac{{4{π^2}R}}{g_0}$B．$\frac{{4{π^2}（R+h）}}{g_0}$C．$\frac{2πh}{R}\sqrt{\frac{h}{g_0}}$D．$\frac{2π（R+h）}{R}\sqrt{\frac{R+h}{g_0}}$

    查看答案和解析>>

    科目：高中物理 来源： 题型：选择题

    20．两个半径为r的，由同种材料制成的均匀球体，球心之间的距离是100r，它们之间万有引力大小是F，则F与r的关系是（　　）
    A．F与r2成反比B．F与r2成正比C．F与r3成正比D．F与r4成正比

    查看答案和解析>>

    同步练习册答案