
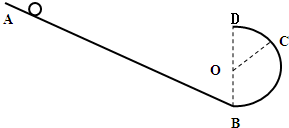
 如图所示,竖直平面内的轨道由足够长的光滑斜面轨道AB和半径为R的光滑半圆形轨道BD连接而成,B为半圆形轨道的最低点,D为半圆形轨道的最高点,重力加速度为g,让质量为m的小球从斜面上某点由静止开始释放:
如图所示,竖直平面内的轨道由足够长的光滑斜面轨道AB和半径为R的光滑半圆形轨道BD连接而成,B为半圆形轨道的最低点,D为半圆形轨道的最高点,重力加速度为g,让质量为m的小球从斜面上某点由静止开始释放:分析 (1)从小球开始运动到到达D点过程机械能守恒,由机械能守恒定律可以求出小球到达D点的速度,在D点由牛顿第二定律可以求出作用力.
(2)求出小球通过最高点时的临界速度,然后应用机械能守恒定律求出释放点的最小高度,然后确定其范围.
(3)由牛顿第二定律求出小球到达C点的速度,然后应用机械能守恒定律求出释放点的高度.
解答 解:(1)小释放小球到D点过程机械能守恒,
由机械能守恒定律得:mg(h1-2R)=$\frac{1}{2}$mv2,
在D点,由牛顿第二定律得:FN+mg=m$\frac{{v}^{2}}{R}$,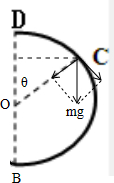
解得:FN=mg;
(2)小释放小球到D点过程机械能守恒,
由机械能守恒定律得:mg(h-2R)=$\frac{1}{2}$mvD2,
小球到达D点速度最小时,重力提供向心力,
在D点,由牛顿第二定律得:mg=m$\frac{{v}_{D}^{2}}{R}$,
解得:h=2.5R,
要使小球能够通过半圆形轨道的最高点D,h≥2.5R;
(3)小球从C点脱离轨道,在C点轨道对小球的作用力为零,受力如图所示:
由几何知识可知:cosθ=$\frac{\frac{5R}{3}-R}{R}$=$\frac{2}{3}$,
在C点,由牛顿第二定律得:mgcosθ=m$\frac{{v}_{C}^{2}}{R}$,
小释放小球到C点过程机械能守恒,
由机械能守恒定律得:mg(h2-$\frac{5R}{3}$)=$\frac{1}{2}$mvC2,
解得:h2=2R;
答:(1)小球通过半圆形轨道的最高点D时轨道对小球的压力FN的大小为mg;
(2)小球的释放点离圆形轨道最低点B的高度h应满足的条件是:h≥2.5R;
(3)小球的释放点离圆形轨道最低点B的高度h2应为2R.
点评 本题考查了机械能守恒定律的应用,分析清楚小球的运动过程,应用机械能守恒定律与牛顿第二定律即可解题,解题时注意小球做圆周运动临界条件的应用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中物理 来源: 题型:选择题
| A. | 与输电线上的电压损失的平方成正比 | |
| B. | 与输送电压的平方成正比 | |
| C. | 与输送电压成反比 | |
| D. | 与输电电流成正比 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 两过程中她都处于超重状态 | B. | 两过程中她都处于失重状态 | ||
| C. | 前过程为超重,后过程为完全失重 | D. | 前过程为完全失重,后过程为超重 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | mg $\sqrt{2gh}$ | B. | mg$\sqrt{2gh}$cosα | C. | mg$\sqrt{2ghsinα}$ | D. | mg$\sqrt{2gh}$sinα |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | $\frac{{v}_{1}}{{v}_{2}}$=$\sqrt{\frac{r}{{r}_{1}}}$ | B. | $\frac{{v}_{1}}{{v}_{2}}$=$\frac{{r}_{1}}{r}$ | C. | $\frac{{a}_{1}}{{a}_{2}}$=$\frac{{r}_{1}^{2}}{{r}^{2}}$ | D. | $\frac{{a}_{1}}{{a}_{2}}$=$\frac{{r}^{2}}{{r}_{1}^{2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com