
| A. | 两行星密度之比为4:1 | |
| B. | 两行星质量之比为32:1 | |
| C. | 两行星表面处重力加速度之比为16:1 | |
| D. | 两卫星的速率之比为$\sqrt{8}$:1 |
分析 研究任一卫星绕行星做匀速圆周运动的情形,根据万有引力提供向心力,列出等式求出行星的质量、卫星的速率,再得到行星的密度.忽略行星自转的影响,根据万有引力等于重力列出等式.再求各个量之比.
解答 解:A、任一卫星绕行星表面做匀速圆周运动时,根据万有引力提供向心力,得:G$\frac{Mm}{{R}^{2}}$=m$\frac{4{π}^{2}}{{T}^{2}}$R
则得行星的质量 M=$\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}$
行星的密度 ρ=$\frac{M}{\frac{4}{3}π{R}^{3}}$=$\frac{3π}{G{T}^{2}}$
两个卫星的周期之比为1:2,由上式可得,两行星密度之比为4:1,故A正确.
B、行星质量为 M=$\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}$,已知两个卫星的周期之比为1:2,两行星半径之比为2:1,由此可得,两行星质量之比为32:1,故B正确.
C、忽略行星自转的影响,根据万有引力等于重力,得 G$\frac{Mm}{{R}^{2}}$=mg,得 g=$\frac{GM}{{R}^{2}}$
结合两行星半径之比为2:1,质量之比为32:1,解得两行星表面处重力加速度之比为8:1,故C错误.
D、根据圆周运动公式 v=$\frac{2πR}{T}$,可得两卫星的速率之比为4:1,故D错误.
故选:AB
点评 对于卫星问题,关键是建立模型,掌握两条基本思路:万有引力等于向心力和万有引力等于重力,运用列式分析比例关系.


科目:高中物理 来源: 题型:选择题
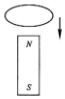 如图,线圈的平面与条形磁铁垂直,且磁铁轴心通过线圈圈心,线圈由高处下落并穿过条形磁铁,在这个过程中,线圈内感应电流的方向自上往下看是( )
如图,线圈的平面与条形磁铁垂直,且磁铁轴心通过线圈圈心,线圈由高处下落并穿过条形磁铁,在这个过程中,线圈内感应电流的方向自上往下看是( )| A. | 逆时针 | B. | 顺时针 | ||
| C. | 先顺时针后逆时针 | D. | 先逆时针后顺时针 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 质点的初速度是5m/s | B. | 质点的加速度是2m/s2 | ||
| C. | 第1 s内的位移是6 m | D. | 质点前2s内的位移是12m |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 10000 W | B. | 1000 W | C. | 100 W | D. | 10 W |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 两列简谐横波分别沿x轴正方向和负方向传播,两波源分别位于x=-0.2m和x=1.2m处,两列波的速度均为v=0.4m/s,两波源的振幅均为A=2cm.如图所示为t=0时刻两列波的图象,波的传播方向在图中已标出,此刻平衡位置处于x=0.2m和x=0.8m的P、Q两质点刚开始振动.质点M的平衡位置处于x=0.5m处,关于各质点运动情况判断正确的是( )
两列简谐横波分别沿x轴正方向和负方向传播,两波源分别位于x=-0.2m和x=1.2m处,两列波的速度均为v=0.4m/s,两波源的振幅均为A=2cm.如图所示为t=0时刻两列波的图象,波的传播方向在图中已标出,此刻平衡位置处于x=0.2m和x=0.8m的P、Q两质点刚开始振动.质点M的平衡位置处于x=0.5m处,关于各质点运动情况判断正确的是( )| A. | t=1s时,质点M的位移为-4cm | B. | t=1s时,质点M的位移为+4cm | ||
| C. | t=0.75s时,质点P、Q都运动到M点 | D. | 质点P、Q的起振方向都沿y轴负方向 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 氢原子跃迁到激发态后,核外电子动能增大,原子的电势能减小 | |
| B. | 基态氢原子中的电子吸收一频率为v的光子被电离后,电子速度大小为$\sqrt{\frac{2(hv-{E}_{1})}{m}}$ | |
| C. | 大量处于n=3的激发态的氢原子,向低能级跃迁时可辐射出3种不同频率的光 | |
| D. | 若原子从n=6能级向n=l能级跃迁时所产生的电磁波能使某金属发生光电效应,则原子从n=6能级向n=2能级跃迁时所产生的电磁波也一定能使该金属发生光电效应 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
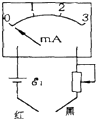 如图所示是把量程为3mA的电流表改装成欧姆表的示意图,其中电源电动势E1=1.5V.改装后若将原电流表3mA刻度处定为零阻值位置,则1.5mA刻度处应标多少500Ω,1mA刻度处应标多少1000Ω.
如图所示是把量程为3mA的电流表改装成欧姆表的示意图,其中电源电动势E1=1.5V.改装后若将原电流表3mA刻度处定为零阻值位置,则1.5mA刻度处应标多少500Ω,1mA刻度处应标多少1000Ω.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 线速度的方向保持不变 | B. | 向心加速度的大小保持不变 | ||
| C. | 合外力保持不变 | D. | 线速度和角速度保持不变 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com