
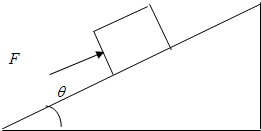
 如图所示,一个质量为m的木块,在平行于斜面向上的推力F作用下,沿着倾角为θ的斜面匀速向上运动,木块与斜面间的动摩擦因数为μ.(μ<tanθ)(已知最大摩擦力等于滑动摩擦力)
如图所示,一个质量为m的木块,在平行于斜面向上的推力F作用下,沿着倾角为θ的斜面匀速向上运动,木块与斜面间的动摩擦因数为μ.(μ<tanθ)(已知最大摩擦力等于滑动摩擦力) 解:(1)受力分析如图所示,可沿斜面向上为x轴正方向,垂直斜面向上为y轴正方向建立直角坐标系,将重力向x轴及y轴分解;
解:(1)受力分析如图所示,可沿斜面向上为x轴正方向,垂直斜面向上为y轴正方向建立直角坐标系,将重力向x轴及y轴分解;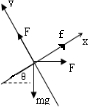







科目:高中物理 来源: 题型:
 如图所示.一个质量为m=10kg的物体,由1/4圆弧轨道上端从静止开始下滑,到达底端时的速度v=2.5m/s,然后沿水平面向右滑动1.0m的距离而停止.已知轨道半径R=0.4m,g=10m/s2,求:
如图所示.一个质量为m=10kg的物体,由1/4圆弧轨道上端从静止开始下滑,到达底端时的速度v=2.5m/s,然后沿水平面向右滑动1.0m的距离而停止.已知轨道半径R=0.4m,g=10m/s2,求:查看答案和解析>>
科目:高中物理 来源: 题型:
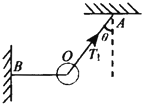 (2007?湖北模拟)如图所示,一个质量为m的小球被AO、BO两根细绳系住,BO绳为水平状态,AO绳与竖直方向的夹角为θ,此时AO绳对小球的拉力大小为T1.烧断BO绳后,小球摆动,当小球再次摆回到图中位置时AO绳对小球的拉力大小为T2.求:
(2007?湖北模拟)如图所示,一个质量为m的小球被AO、BO两根细绳系住,BO绳为水平状态,AO绳与竖直方向的夹角为θ,此时AO绳对小球的拉力大小为T1.烧断BO绳后,小球摆动,当小球再次摆回到图中位置时AO绳对小球的拉力大小为T2.求:查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,一个质量为m,电荷量为q的带负电的粒子(重力不计),以初速度v由狭缝S1,垂直进入电场强度为E的匀强电场中.
如图所示,一个质量为m,电荷量为q的带负电的粒子(重力不计),以初速度v由狭缝S1,垂直进入电场强度为E的匀强电场中.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com