
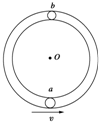
 如图所示光滑管形圆轨道半径为R(管径远小于R),小球a、b大小相同,质量相同,均为m,其直径略小于管径,能在管中无摩擦运动.两球先后以相同速度v通过轨道最低点,且当小球a在最低点时,小球b在最高点,以下说法正确的是
如图所示光滑管形圆轨道半径为R(管径远小于R),小球a、b大小相同,质量相同,均为m,其直径略小于管径,能在管中无摩擦运动.两球先后以相同速度v通过轨道最低点,且当小球a在最低点时,小球b在最高点,以下说法正确的是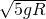 ,才能使两球在管内做圆周运动?
,才能使两球在管内做圆周运动?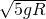 时,小球b在轨道最高点对轨道无压力?
时,小球b在轨道最高点对轨道无压力?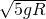 ,小球a对轨道最低点压力比小球b对轨道最高点压力都大6mg
,小球a对轨道最低点压力比小球b对轨道最高点压力都大6mg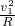 ;
;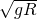 ;即当速度为
;即当速度为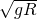 时,小球在轨道最高点对轨道无压力;
时,小球在轨道最高点对轨道无压力; mv22-
mv22- mv12;
mv12;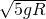 ,故最低点速度至少为
,故最低点速度至少为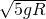 ,才能使两球在管内做圆周运动;当速度为
,才能使两球在管内做圆周运动;当速度为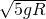 时,小球在最高点对轨道无压力;故B正确;
时,小球在最高点对轨道无压力;故B正确;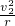 =5mg;即a球比b球所需向心力大4mg;故C错误;
=5mg;即a球比b球所需向心力大4mg;故C错误;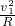 ;解得T1=m
;解得T1=m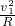 -mg;
-mg;  ;解得T2=m
;解得T2=m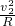 +mg;
+mg;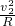 -
-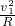 ;
; mv22-
mv22- mv12;
mv12;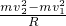 =4mg;
=4mg;

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中物理 来源: 题型:
 如图所示光滑管形圆轨道半径为R(管径远小于R),小球a、b大小相同,质量相同,均为m,其直径略小于管径,能在管中无摩擦运动.两球先后以相同速度v通过轨道最低点,且当小球a在最低点时,小球b在最高点,以下说法正确的是( )
如图所示光滑管形圆轨道半径为R(管径远小于R),小球a、b大小相同,质量相同,均为m,其直径略小于管径,能在管中无摩擦运动.两球先后以相同速度v通过轨道最低点,且当小球a在最低点时,小球b在最高点,以下说法正确的是( )查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示光滑管形圆轨道半径为R(管径远小于R),小球a、b大小相同,质量均为m,其直径略小于管径,能在管中无摩擦运动.两球先后以相同速度v通过轨道最低点,且当小球a在最低点时,小球b在最高点,以下说法正确的是( )
如图所示光滑管形圆轨道半径为R(管径远小于R),小球a、b大小相同,质量均为m,其直径略小于管径,能在管中无摩擦运动.两球先后以相同速度v通过轨道最低点,且当小球a在最低点时,小球b在最高点,以下说法正确的是( )查看答案和解析>>
科目:高中物理 来源: 题型:
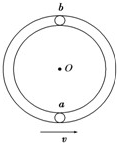 如图所示光滑管形圆轨道半径为R(管径远小 于R),小球a、b大小相同,质量均为m,其直径略小于管径,能在管中无摩擦运动.两球先后以相同速度v通过轨道最低点,且当小球a在最低点时,小球b在最高点,以下说法正确的是( )
如图所示光滑管形圆轨道半径为R(管径远小 于R),小球a、b大小相同,质量均为m,其直径略小于管径,能在管中无摩擦运动.两球先后以相同速度v通过轨道最低点,且当小球a在最低点时,小球b在最高点,以下说法正确的是( )查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示光滑管形圆轨道半径为R(管径远小于R),小球a、b大小相同,质量均为m,其直径略小于管径,能在管中无摩擦运动.两球先后以相同速度v通过轨道最低点,且当小球a在最低点时,小球b在最高点,以下说法正确的是( )
如图所示光滑管形圆轨道半径为R(管径远小于R),小球a、b大小相同,质量均为m,其直径略小于管径,能在管中无摩擦运动.两球先后以相同速度v通过轨道最低点,且当小球a在最低点时,小球b在最高点,以下说法正确的是( )查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示光滑管形圆轨道半径为R(管径远小于R)固定,小球a、b大小相同,质量相同,均为m,其直径略小于管径,能在管中无摩擦运动.两球先后以相同速度v通过轨道最低点,且当小球a在最低点时,小球b在最高点,以下说法正确的是( )
如图所示光滑管形圆轨道半径为R(管径远小于R)固定,小球a、b大小相同,质量相同,均为m,其直径略小于管径,能在管中无摩擦运动.两球先后以相同速度v通过轨道最低点,且当小球a在最低点时,小球b在最高点,以下说法正确的是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com