
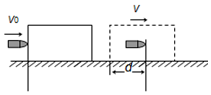
 设质量为m的子弹以初速度v0射向静止在光滑水平面上的质量为M的木块,并留在木块中不再射出,子弹钻入木块深度为d.
设质量为m的子弹以初速度v0射向静止在光滑水平面上的质量为M的木块,并留在木块中不再射出,子弹钻入木块深度为d.分析 ①子弹与木块组成的系统动量守恒,由动量守恒定律求出子弹与木块的共同速度;
②产生的热能等于系统的动能减少量,由能量守恒定律求.
③由功能关系知,产生热能 Q=fd,即可求出平均阻力f的大小.
解答 解:①子弹射入木块的过程中,系统动量守恒,取水平向右为正方向,由动量守恒定律得:
mv0=(M+m)v,
解得共同速度为:v=$\frac{m{v}_{0}}{M+m}$;
②该过程系统损失的动能全部转化为系统的内能,根据能量守恒定律得:
产生的热能 Q=$\frac{1}{2}$mv02-$\frac{1}{2}$(M+m)v2,
解得:Q=$\frac{Mm{v}_{0}^{2}}{2(M+m)}$
③设平均阻力大小为f,据功能关系得:Q=fd
则 f=$\frac{Mm{v}_{0}^{2}}{2(M+m)d}$
答:
①木块最终速度的大小是$\frac{m{v}_{0}}{M+m}$;
②产生的热能是$\frac{Mm{v}_{0}^{2}}{2(M+m)}$;
③平均阻力的大小是$\frac{Mm{v}_{0}^{2}}{2(M+m)d}$.
点评 本题要注意分析清楚物体的运动过程,抓住打击的基本规律:系统的动量守恒和能量守恒是关键,要知道产生的热能与相对位移即子弹钻入木块的深度有关.


科目:高中物理 来源: 题型:多选题
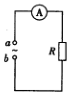 如图所示,电路中电阻的阻值 R=100Ω,电流表为理想电流表,在a、b之间接入电压 U=220$\sqrt{2}$sin100πt(V)的交流电源,则( )
如图所示,电路中电阻的阻值 R=100Ω,电流表为理想电流表,在a、b之间接入电压 U=220$\sqrt{2}$sin100πt(V)的交流电源,则( )| A. | 电流表的示数为2.2 A | |
| B. | t=0.01 s时,电流表的示数为零 | |
| C. | 若产生该交流电的发电机的线框转速提高一倍,其他条件不变,则电流表的示数也增大一倍 | |
| D. | 若将电阻换成200,则电源的输出功率变为原来的两倍 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 在任何情况下都不对 | B. | 对于各自选定的参照系都对 | ||
| C. | 对于选定的同一参照系都对 | D. | 总有一个人或两个人是讲错的 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
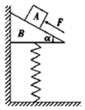 如图所示,物块A放在直角三角形斜面体B上面,B放在弹簧上面并紧挨着竖直墙壁,初始时A、B静止;现用力F沿斜面向上推A,但A、B仍未动.则施力F后,下列说法不正确的是( )
如图所示,物块A放在直角三角形斜面体B上面,B放在弹簧上面并紧挨着竖直墙壁,初始时A、B静止;现用力F沿斜面向上推A,但A、B仍未动.则施力F后,下列说法不正确的是( )| A. | A、B之间的摩擦力一定变大 | B. | B与墙面的弹力可能不变 | ||
| C. | B与墙之间可能没有摩擦力 | D. | 弹簧弹力一定不变 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
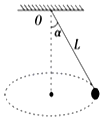 长为L=1m的细线,拴一质量为m=2kg的小球,一端固定于O点.让其在水平面内做匀速圆周运动(这种运动通常称为圆锥摆运动),如图.求摆线L与竖直方向的夹角为α=53°时:
长为L=1m的细线,拴一质量为m=2kg的小球,一端固定于O点.让其在水平面内做匀速圆周运动(这种运动通常称为圆锥摆运动),如图.求摆线L与竖直方向的夹角为α=53°时:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,虚线表示某点电荷Q所激发电场的等势面,已知a、b两点在同一等势面上,c、d两点在另一个等势面上.甲、乙两个带电粒子以相同的速率,沿不同的方向从同一点a射入电场,在电场中沿不同的轨迹adb曲线、acb曲线运动.则下列说法正确( )
如图所示,虚线表示某点电荷Q所激发电场的等势面,已知a、b两点在同一等势面上,c、d两点在另一个等势面上.甲、乙两个带电粒子以相同的速率,沿不同的方向从同一点a射入电场,在电场中沿不同的轨迹adb曲线、acb曲线运动.则下列说法正确( )| A. | 两粒子所带的电荷符号不同 | |
| B. | 甲粒子经过c点时的速度一定小于乙粒子经过d点的速度 | |
| C. | 两个粒子的电势能都是先减小后增大 | |
| D. | 经过b点时,两粒子的动能一定相等 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示的竖直直角坐标平面xoy内有两条过原点的射线OA和OB与x轴的正半轴和负半轴都成45°角,在x轴上方∠AOB区域间分布着方向垂直纸面向外大小为B1的匀强磁场,在x轴的下方存在着方向垂直纸面向外大小为B2=$\frac{mv}{qL}$匀强磁场,现有一质量为m,带电量为+q的带电粒子以速度v从位于直线OA上的P(L,L)点竖直向下射出,经过测量发现,此粒子每经过相同的时间T会回到P点,(不计粒子重力)
如图所示的竖直直角坐标平面xoy内有两条过原点的射线OA和OB与x轴的正半轴和负半轴都成45°角,在x轴上方∠AOB区域间分布着方向垂直纸面向外大小为B1的匀强磁场,在x轴的下方存在着方向垂直纸面向外大小为B2=$\frac{mv}{qL}$匀强磁场,现有一质量为m,带电量为+q的带电粒子以速度v从位于直线OA上的P(L,L)点竖直向下射出,经过测量发现,此粒子每经过相同的时间T会回到P点,(不计粒子重力)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com