
 滑板运动受到青少年的追棒,如图是某滑板运动员在一次表演时的一部分赛道在竖直平面内的示意图.DB段为光滑的四分之一圆弧,AB段水平且粗糙恰与圆弧DB在B点相切,赛道固定在水平面上.一个质量为m的运动员(可视为质点)从赛道的A端以初动能E冲上水平赛道AB,并沿着赛道运动,然后由DB弧滑下后停在赛道AB段的中点.已知AB长为L,重力加速度为g,求:
滑板运动受到青少年的追棒,如图是某滑板运动员在一次表演时的一部分赛道在竖直平面内的示意图.DB段为光滑的四分之一圆弧,AB段水平且粗糙恰与圆弧DB在B点相切,赛道固定在水平面上.一个质量为m的运动员(可视为质点)从赛道的A端以初动能E冲上水平赛道AB,并沿着赛道运动,然后由DB弧滑下后停在赛道AB段的中点.已知AB长为L,重力加速度为g,求:分析 (1)对全程由动能定理可求得动摩擦因数;
(2)对到达D过程由动能定理可求得圆弧半径的最小值;
(3)对冲上轨道过程由动能定理及功能关系可求得运动员的最终位置.
解答 解:(1)运动员最终停在AB的中点,在此过程中,由动能定理可得:
-μmg(L+$\frac{L}{2}$)=-E
解得:μ=$\frac{2E}{3mgL}$;
(2)若运动员刚好到达D处,速度为零,由动能定理可得:
-μmgL-mgR=-E
解得BD圆弧半径至少为R=$\frac{E}{3mg}$;
(3)设运动员以初动能E′冲上轨道,可以达到最大高度为1.5R
由动能定理得:
-μmgL-1.5mgR=-E′
解得:E′=$\frac{7E}{6}$
运动员滑回B点时的动能为EB=1.5mgR=$\frac{E}{2}$;
由于EB<μmgL=$\frac{2}{3}$E
故运动员将停在轨道上;
答:(1)运动员的鞋底滑板与水平赛道AB间的动摩擦因数μ为$\frac{2E}{3mgL}$.
(2)为了保证运动员不从D端离开赛道,圆弧DB段的半径R至少是$\frac{E}{3mg}$;
(3)最后停在水平赛道AB上.
点评 本题考查动量守恒定律及匀速直线运动规律,要注意正确选择研究对象及物理过程进行分析,才能正确选择物理规律求解.


科目:高中物理 来源: 题型:选择题
| A. | “CX”的速度是地球同步卫星速度的$\sqrt{5}$倍 | |
| B. | “CX”的加速度是地球同步卫星加速度的5倍 | |
| C. | “CX”相对于地球赤道上的观测者向西运动 | |
| D. | “CX”要实现对更低轨道上“垃圾卫星”的拯救必须直接加速 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
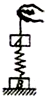 如图所示,物体A和B的质量为m,它们通过一劲度系数为k的轻弹簧相连,开始时B放在地面上,A、B都处于静止状态,现用手通过细绳缓慢地将A向上提升距离为L1时,B刚要离开地面,此过程手做功为W1;若将A加速向上提起,A上升的距离为L2时,B刚要离开地面,此时A的速度为v,此过程手做功为W2,弹簧一直处于弹性限度内,则( )
如图所示,物体A和B的质量为m,它们通过一劲度系数为k的轻弹簧相连,开始时B放在地面上,A、B都处于静止状态,现用手通过细绳缓慢地将A向上提升距离为L1时,B刚要离开地面,此过程手做功为W1;若将A加速向上提起,A上升的距离为L2时,B刚要离开地面,此时A的速度为v,此过程手做功为W2,弹簧一直处于弹性限度内,则( )| A. | L1=L2=$\frac{mg}{k}$ | B. | W2>W1 | C. | W1=mgL1 | D. | W2=mgL2+$\frac{m{v}^{2}}{2}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | $\frac{3{v}^{3}{t}^{4}}{16G{t}_{1}^{3}{π}^{4}{n}^{4}}$ | B. | $\frac{3\sqrt{3}{v}^{3}{t}^{4}}{16G{{t}_{1}}^{3}{π}^{4}{n}^{4}}$ | ||
| C. | $\frac{3{v}^{2}{t}^{4}}{16G{t}_{1}^{3}{π}^{4}{n}^{4}}$ | D. | $\frac{3\sqrt{3}{v}^{2}{t}^{4}}{16G{{t}_{1}}^{3}{π}^{4}{n}^{4}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 由玻尔理论可知,氢原子的核外电子由较高能级跃迁到较低能级时,要释放一定频率的光子,同时电子的动能减小,电势能增大 | |
| B. | 对于同一种金属来说,其极限频率恒定,与入射光的频率及光的强度均无关 | |
| C. | 比结合能越大表示原子核中的核子结合得越牢固 | |
| D. | 通过α粒子散射实验可以估算原子核的大小 | |
| E. | 太阳内部发生的核反应是${\;}_{92}^{235}$U+${\;}_{0}^{1}$n→${\;}_{56}^{144}$Ba+${\;}_{36}^{89}$Kr+3${\;}_{0}^{1}$n |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
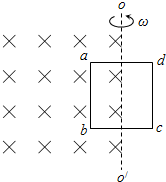 如图所示,单匝矩形闭合导线框abcd一半处于磁感应强度为B的水平有界匀强磁场中,线框面积为S,电阻为R.线框绕与其中心线重合的竖直固定转轴OO′以角速度ω匀速转动,固定转轴恰好位于匀强磁场的右边界.则线框中感应电流的有效值为( )
如图所示,单匝矩形闭合导线框abcd一半处于磁感应强度为B的水平有界匀强磁场中,线框面积为S,电阻为R.线框绕与其中心线重合的竖直固定转轴OO′以角速度ω匀速转动,固定转轴恰好位于匀强磁场的右边界.则线框中感应电流的有效值为( )| A. | $\frac{{\sqrt{2}Bsω}}{4R}$ | B. | $\frac{{\sqrt{2}Bsω}}{2R}$ | C. | $\frac{Bsω}{4R}$ | D. | $\frac{Bsω}{2R}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 布朗运动就是液体分子的无规则运动 | |
| B. | 当两分子间距离增大时,分子力一定减小而分子势能一定增加 | |
| C. | 热量不会自动地从低温物体传给高温物体而不引起其他变化 | |
| D. | 夏天将密闭有空气的矿泉水瓶放进低温的冰箱中会变扁,此过程中瓶内空气(可看成理想气体)的内能减小,外界对其做功同时向外放热 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 已知阿伏加德罗常数、气体摩尔质量和密度,可算出该气体分子间的平均距离 | |
| B. | 为了保存玉米地的水分,可以锄松地面,破坏土壤里的毛细管 | |
| C. | 随着分子间距离的增大,分子间的引力和斥力都减小,但斥力减小得快,合力表现为引力 | |
| D. | 物质是晶体还是非晶体,比较可靠的办法是从各向异性或各向同性来判断 | |
| E. | 能量耗散从能量角度反映出自然界的宏观过程具有方向性 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com