
 ČēĶ¼ĖłŹ¾£¬ÖŹĮæĪŖMµÄľæé¾²Ö¹ŌŚ¹ā»¬Ė®Ę½ĆęÉĻ£¬Óė¹Ģ¶ØŌŚŹśÖ±Ē½ĆęÉĻµÄĒįÖŹµÆ»É½ōææŌŚŅ»Ęšµ«²»Õ³Į¬£®ŅŌÖŹĮæĪŖmµÄ×ÓµÆĖ®Ę½ÉäČėľæé²¢Ē¶ČėĘäÖŠ£¬ŅŃÖŖ×ÓµÆÉäČėľæéĒ°Ė²¼äµÄĖŁ¶ČĪŖv0£¬µÆ»ÉŹ¼ÖÕŌŚµÆŠŌĻŽ¶ČÄŚ£®Ōņ“Ó×ÓµÆæŖŹ¼ÉäČėľæ鵽ľæé×īÖÕÓėµÆ»É·ÖĄėµÄ¹ż³ĢÖŠ£¬ĻĀĮŠĖµ·ØÕżČ·µÄŹĒ£Ø””””£©
ČēĶ¼ĖłŹ¾£¬ÖŹĮæĪŖMµÄľæé¾²Ö¹ŌŚ¹ā»¬Ė®Ę½ĆęÉĻ£¬Óė¹Ģ¶ØŌŚŹśÖ±Ē½ĆęÉĻµÄĒįÖŹµÆ»É½ōææŌŚŅ»Ęšµ«²»Õ³Į¬£®ŅŌÖŹĮæĪŖmµÄ×ÓµÆĖ®Ę½ÉäČėľæé²¢Ē¶ČėĘäÖŠ£¬ŅŃÖŖ×ÓµÆÉäČėľæéĒ°Ė²¼äµÄĖŁ¶ČĪŖv0£¬µÆ»ÉŹ¼ÖÕŌŚµÆŠŌĻŽ¶ČÄŚ£®Ōņ“Ó×ÓµÆæŖŹ¼ÉäČėľæ鵽ľæé×īÖÕÓėµÆ»É·ÖĄėµÄ¹ż³ĢÖŠ£¬ĻĀĮŠĖµ·ØÕżČ·µÄŹĒ£Ø””””£©| A£® | µÆ»É¶Ōľæé×öµÄ¹¦ĪŖ0 | |
| B£® | µÆ»É¶Ōľæé³åĮæµÄ“óŠ”ĪŖ0 | |
| C£® | ×ÓµÆÓėľæé×é³ÉµÄĻµĶ³¶ÆĮæŹŲŗć | |
| D£® | Õūøö¹ż³ĢÖŠĖšŹ§µÄ»śŠµÄÜĪŖ$\frac{Mm}{2£ØM+m£©}$${v}_{0}^{2}$ |
·ÖĪö øł¾ŻŠĪ±äĮæ·ÖĪöµÆ»É¶Ōľæé×ö¹¦µÄ“󊔣®øł¾Ż¶ÆĮæ¶ØĄķ·ÖĪöµÆ»É¶Ōľæé³åĮæµÄ“󊔣®øł¾Ż¶ÆĮæŹŲŗćµÄĢõ¼ž£ŗŗĻĶāĮ¦ĪŖĮć£¬ÅŠ¶ĻĻµĶ³µÄ¶ÆĮæŹĒ·ńŹŲŗć£»Ó¦ÓƶÆĮæŹŲŗć¶ØĀÉÓė»śŠµÄÜŹŲŗć¶ØĀÉæÉĒóĖšŹ§µÄ»śŠµÄÜ£®
½ā“š ½ā£ŗA”¢“Ó×ÓµÆæŖŹ¼ÉäČėľæ鵽ľæé×īÖÕÓėµÆ»É·ÖĄėµÄ¹ż³ĢÖŠ£¬µÆ»É³õĢ¬ŗĶÄ©Ģ¬¶¼“¦ÓŚŌ³¤×“Ģ¬£¬³õĩדĢ¬µÆ»ÉµÄµÆŠŌŹĘÄÜĻąµČ£¬ŌņµÆ»É¶Ōľæé×öµÄ¹¦ĪŖ0£¬¹ŹAÕżČ·£®
B”¢Éč×ÓµÆÉäČėľæéŗóµÄĖ²¼ä£¬×ÓµÆŗĶľæéµÄ¹²Ķ¬ĖŁ¶Č“óŠ”ĪŖv£®Č”Ļņ×óĪŖÕż·½Ļņ£¬¶Ō×ÓµÆŗĶľæéÕūĢ壬øł¾Ż¶ÆĮæ¶ØĄķµĆµÆ»É¶Ōľæé³åĮæĪŖ£ŗ
I=-£ØM+m£©v-£ØM+m£©v=-2£ØM+m£©v£¬¹ŹB“ķĪó£®
C”¢ŅŌ×ӵƔ¢µÆ»É”¢Ä¾æé¹¹³ÉµÄĻµĶ³ĪŖŃŠ¾æ¶ŌĻó£¬Ē½¶ŌµÆ»ÉÓŠ×÷ÓĆĮ¦£¬ĻµĶ³ĖłŹÜŗĻĶāĮ¦²»ĪŖĮć£¬¹ŹĻµĶ³¶ÆĮæ²»ŹŲŗć£¬¹ŹC“ķĪó£®
D”¢Č”Ļņ×óĪŖÕż·½Ļņ£¬øł¾Ż¶ÆĮæŹŲŗć¶ØĀÉµĆ mv0=£ØM+m£©v£¬Õūøö¹ż³ĢÖŠĖšŹ§µÄ»śŠµÄÜĪŖ”÷E=$\frac{1}{2}$mv02-$\frac{1}{2}$£ØM+m£©v2=$\frac{Mm}{2£ØM+m£©}$${v}_{0}^{2}$£¬¹ŹDÕżČ·£®
¹ŹŃ”£ŗAD
µćĘĄ ±¾ĢāµÄ¹Ų¼üŹĒĆ÷Č·ĻµĶ³µÄ¶ÆĮæŹŲŗćµÄĢõ¼žŗĶ»śŠµÄÜŹŲŗćµÄĢõ¼ž£¬Č»ŗóŌĖÓƶÆĮæŹŲŗć¶ØĀÉŗĶ»śŠµÄÜŹŲŗć¶ØĀÉĮŠŹ½Ēó½ā£®


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗøßÖŠĪļĄķ Ą“Ō“£ŗ ĢāŠĶ£ŗŹµŃéĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠĪļĄķ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | ĪļĢåŌŚ$\frac{t}{2}$Ź±æĢµÄĖ²Ź±ĖŁ¶ČŹĒ$\frac{2L}{t}$ | |
| B£® | ĪļĢåČ«¹ż³ĢµÄĘ½¾łĖŁ¶ČŹĒ$\frac{L}{t}$ | |
| C£® | ĪļĢåµ½Š±ĆęÖŠµćŹ±µÄĖ²Ź±ĖŁ¶ČŠ”ÓŚ$\frac{L}{t}$ | |
| D£® | ĪļĢå“ÓæŖŹ¼ŌĖ¶Æµ½Š±ĆęÖŠµć¾ĄśµÄŹ±¼äĪŖ$\frac{t}{2}$ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠĪļĄķ Ą“Ō“£ŗ ĢāŠĶ£ŗ¼ĘĖćĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠĪļĄķ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠĪļĄķ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
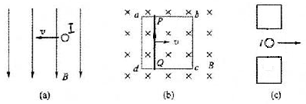
| A£® | ĒŠĻߊ±ĻņÉĻŹ±Ę«“󣬊±ĻņĻĀŹ±Ę«Š” | B£® | ĒŠĻߊ±ĻņÉĻŹ±Ę«Š”£¬Š±ĻņĻĀŹ±Ę«“ó | ||
| C£® | ĒŠĻߊ±ĻņÉĻ»ņŠ±ĻņĻĀ¾łĘ«Š” | D£® | ĒŠĻߊ±ĻņÉĻ»ņŠ±ĻņĻĀ¾łĘ«“ó |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠĪļĄķ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
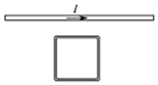 ČēĶ¼ĖłŹ¾£¬¹Ģ¶ØµÄĖ®Ę½³¤Ö±µ¼ĻßÖŠĶØÓŠµēĮ÷I£¬¾ŲŠĪĻßæņÓėµ¼ĻßŌŚĶ¬Ņ»ŹśÖ±Ę½ĆęÄŚ£¬ĒŅŅ»±ßÓėµ¼ĻßĘ½ŠŠ£®ĻßæņÓɾ²Ö¹ŹĶ·Å£¬²»¼ĘæÕĘų×čĮ¦£¬ŌŚĻĀĀä¹ż³ĢÖŠ
ČēĶ¼ĖłŹ¾£¬¹Ģ¶ØµÄĖ®Ę½³¤Ö±µ¼ĻßÖŠĶØÓŠµēĮ÷I£¬¾ŲŠĪĻßæņÓėµ¼ĻßŌŚĶ¬Ņ»ŹśÖ±Ę½ĆęÄŚ£¬ĒŅŅ»±ßÓėµ¼ĻßĘ½ŠŠ£®ĻßæņÓɾ²Ö¹ŹĶ·Å£¬²»¼ĘæÕĘų×čĮ¦£¬ŌŚĻĀĀä¹ż³ĢÖŠ| A£® | “©¹żĻßæņµÄ“ÅĶØĮæ±£³Ö²»±ä | B£® | ĻßæņĖłŹÜ°²ŽåĮ¦µÄŗĻĮ¦ĪŖĮć | ||
| C£® | ĻßæņÖŠøŠÓ¦µēĮ÷·½Ļņ±£³Ö²»±ä | D£® | ĻßæņµÄ»śŠµÄܲ»¶ĻŌö“ó |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠĪļĄķ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | ŌĀĒņµÄÖŹĮæĪŖ$\frac{{4{¦Š^2}{{£Ø{R+h}£©}^3}}}{{G{T^2}}}$ | |
| B£® | ŌĀĒņµÄµŚŅ»ÓīÖęĖŁ¶ČĪŖ$\frac{2¦Š}{T}\sqrt{\frac{{{{£ØR+h£©}^3}}}{R}}$ | |
| C£® | ”°ęĻ¶šČżŗÅ”±ČĘŌĀŌĖŠŠŹ±µÄĻņŠÄ¼ÓĖŁ¶ČĪŖ$\frac{{4{¦Š^2}R}}{T^2}$ | |
| D£® | ĪļĢåŌŚŌĀĒņ±ķĆę×ŌÓÉĻĀĀäµÄ¼ÓĖŁ¶Č“óŠ”ĪŖ$\frac{{4{¦Š^2}{{£ØR+h£©}^3}}}{{{R^2}{T^2}}}$ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠĪļĄķ Ą“Ō“£ŗ ĢāŠĶ£ŗ¼ĘĖćĢā
 ČēĶ¼ĖłŹ¾£¬ÉČŠĪAOBĪŖĶøĆ÷ֳד½éÖŹµÄŗį½ŲĆę£¬Ō²ŠÄ½Ē”ĻAOB=60”ć£®Ņ»ŹųĘ½ŠŠÓŚ½ĒĘ½·ÖĻßOMĆęµÄµ„É«¹āÓÉOAĆęÉäČė½éÖŹ£¬¾OAĆęÕŪÉäµÄ¹āĻßĒ”Ę½ŠŠÓŚĆęOB£®
ČēĶ¼ĖłŹ¾£¬ÉČŠĪAOBĪŖĶøĆ÷ֳד½éÖŹµÄŗį½ŲĆę£¬Ō²ŠÄ½Ē”ĻAOB=60”ć£®Ņ»ŹųĘ½ŠŠÓŚ½ĒĘ½·ÖĻßOMĆęµÄµ„É«¹āÓÉOAĆęÉäČė½éÖŹ£¬¾OAĆęÕŪÉäµÄ¹āĻßĒ”Ę½ŠŠÓŚĆęOB£®²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com