
 ��ͼ��ʾ������ϵ��x����ˮƽ����y������ֱ������x���Ϸ��ռ�ĵڶ������ڣ���һ����ֱ���µ���ǿ�糡���ڵ������ޣ�������y�����������ǿ�糡�ʹ�ֱxyƽ�棨ֽ�棩�������ǿ�ų����ڵ�һ���������ޣ���������x��������н�Ϊ30�����ǿ�糡���ĸ����ĵ糡ǿ�ȴ�С����ȣ�һ����Ϊm������Ϊ+q�Ĵ����ʵ㣬��y����y=h����p����һ����ˮƽ���ٶ���x�Ḻ�������ڶ����ޣ�Ȼ��x����x=-2h����p�����������ޣ������ʵ�ǡ����������Բ���˶���֮��y����y=-2h����p�����������ޣ���֪�������ٶ�Ϊg����
��ͼ��ʾ������ϵ��x����ˮƽ����y������ֱ������x���Ϸ��ռ�ĵڶ������ڣ���һ����ֱ���µ���ǿ�糡���ڵ������ޣ�������y�����������ǿ�糡�ʹ�ֱxyƽ�棨ֽ�棩�������ǿ�ų����ڵ�һ���������ޣ���������x��������н�Ϊ30�����ǿ�糡���ĸ����ĵ糡ǿ�ȴ�С����ȣ�һ����Ϊm������Ϊ+q�Ĵ����ʵ㣬��y����y=h����p����һ����ˮƽ���ٶ���x�Ḻ�������ڶ����ޣ�Ȼ��x����x=-2h����p�����������ޣ������ʵ�ǡ����������Բ���˶���֮��y����y=-2h����p�����������ޣ���֪�������ٶ�Ϊg�������� ��1�����ݵ糡����������ȣ������������ṩ����������ţ�ٵڶ��������˶�ѧ��ʽ��������⣻
��2���������������ṩ����������ϼ��ι�ϵ���������ų���
��3�����˶����зֽ⣬���ʸ���ϳɷ��������˶�ѧ��ʽ��������⣮
��� �⣺��1����������ĵ糡ǿ�ȴ�СΪE��
�����ӽ����������ǡ����������Բ���˶�֪��Eq=mg
��ã�E=$\frac{mg}{q}$��
�ڵڶ�������ֱ������ٶ�a2=$\frac{mg+qE}{m}$=2g
��ôˮƽ����2h=v0t1
��ֱ����h=$\frac{1}{2}$a2t12��
���v0=2$\sqrt{gh}$
t1=$\sqrt{\frac{h}{g}}$
��ֱ����vy=2gt1=2$\sqrt{gh}$
���V=$\sqrt{{v}_{x}^{2}+{v}_{y}^{2}}$=2$\sqrt{2gh}$
��x�Ḻ��нǦȣ���tan��=$\frac{{v}_{y}}{{v}_{x}}$=1��
��ã���=45�㣻
��2������������������͵糡���������ų����ṩ������BqV=$\frac{m{V}^{2}}{r}$��
���ɼ���֪ʶ֪p2p3ΪԲ�ܵ�ֱ����
����r=$\sqrt{2}$h
��ã�B=$\frac{2m\sqrt{gh}}{qh}$
��3�����ӽ������������ֱ���µ�����СFy=Eqsin30��+mg
��ֱ���¼��ٶȴ�Сay=$\frac{3}{2}g$
��������ֱ���ϵ��ٶ�Ϊ0ʱ��x�����
��vy=Vcos45��-ayt2=0
t2=$\frac{4\sqrt{gh}}{3g}$
�����������������߶�H=Vcos45��t2-$\frac{1}{2}{a}_{4}{t}_{2}^{2}$
��ã�H=$\frac{4}{3}h$
��ô��x������ľ���y=2h-H=$\frac{2}{3}h$
��ˮƽ������ٶȴ�Сax=$\frac{\sqrt{3}}{2}g$
��ˮƽ�������Ҿ���Ϊx=vsin45��t2+$\frac{1}{2}{a}_{x}{t}_{2}^{2}$=$\frac{8h}{3}+\frac{4\sqrt{3}}{9}h$
�ʾ�ԭ��O�ľ���s=$\sqrt{{x}^{2}+{y}^{2}}=\frac{2\sqrt{165+48\sqrt{3}}}{9}h$��
�𣺣�1�����ӵ���p��ʱ�ٶȵĴ�С2$\sqrt{2gh}$�ͷ�����x�Ḻ��н�45�㣻
��2���糡ǿ��$\frac{mg}{q}$�ʹŸ�Ӧǿ�ȵĴ�С$\frac{2m\sqrt{gh}}{qh}$��
��3���������ʵ��ڽ������������x�����ʱ��ԭ��O�ľ���$\frac{2\sqrt{165+48\sqrt{3}}}{9}h$��
���� ���������ڵ糡��ų��˶���������ƽ���˶�������Բ���˶��������˶��ĺϳ���ֽ⣬������ƽ���˶��Ĺ��ɣ�


 ����˼ά�żӿ���ϵ�д�
����˼ά�żӿ���ϵ�д� �����Ծ�ϵ�д�
�����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������
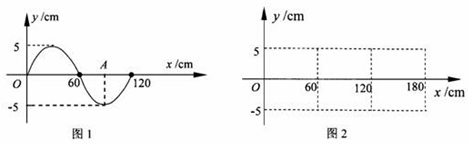
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
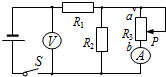
| A�� | ��ѹ��ʾ������ | B�� | ��ѹ��ʾ����С | C�� | ������ʾ������ | D�� | ������ʾ����С |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ������Ϊm�Ĺ⻬С������б���ϣ���һ����ֱ�̶���б���ϵĵ��嵲ס����ʹб����ˮƽ�������������ٶ�Ϊa���ȼ���ֱ���˶������з�����ȷ���ǣ�������
��ͼ��ʾ������Ϊm�Ĺ⻬С������б���ϣ���һ����ֱ�̶���б���ϵĵ��嵲ס����ʹб����ˮƽ�������������ٶ�Ϊa���ȼ���ֱ���˶������з�����ȷ���ǣ�������| A�� | �����ٶ��㹻С����ֱ�������ĵ�������Ϊ�� | |
| B�� | �����ٶ��㹻��б�����ĵ�������Ϊ�� | |
| C�� | б��͵������ĵ����ĺ�������ma | |
| D�� | ���ٶ���a������2a�Ĺ����У�б�����ĵ������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ţ�ٵ�һ������ţ�ٵڶ����ɵ�һ������ | |
| B�� | ţ�ٵڶ��������о������˶�������ʱ������ | |
| C�� | ������֮����������ͷ���������һ��ƽ���� | |
| D�� | Ϊ����ţ�٣����ǰѡ���������Ϊ����������������ʵ�λ�ǡ�ţ�١� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� |  ţ�ٸ�������б��ʵ�飬���������ά�������˶���ԭ�� | |
| B�� |  ���ĵ���ͨ��Ť��ʵ�飬���ɳ��������������� | |
| C�� | 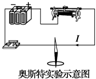 ��˹��ͨ��ʵ���о��������˵�����Χ���ڴų� | |
| D�� |  ������ͨ��ʵ���о����ܽ����Ÿ�Ӧ�����и�Ӧ��������Ĺ��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
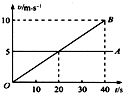
| A�� | 30sĩB�˶���Aǰ�� | B�� | A�������˶���B���ȼ����˶� | ||
| C�� | 20sĩA��B���� | D�� | 40sĩA��B���� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com