
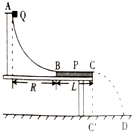
 ��ͼ��ʾ��AB�ǰ뾶ΪR���ķ�֮һ�⻬Բ���������ˮƽ�̶����õ�P����ϱ���BC��B�����У�BC�ij���ΪL��C����ˮƽ����Ĵ�ֱͶӰΪC�䣬CC��ĸ߶�Ϊh��һС��飨����Ϊ�ʵ㣩Q�ӹ���ϵ�A���ɾ�ֹ�ͷţ��������D�㣬C��D�ľ���Ϊs���������ٶ�Ϊg�����ƿ�����������
��ͼ��ʾ��AB�ǰ뾶ΪR���ķ�֮һ�⻬Բ���������ˮƽ�̶����õ�P����ϱ���BC��B�����У�BC�ij���ΪL��C����ˮƽ����Ĵ�ֱͶӰΪC�䣬CC��ĸ߶�Ϊh��һС��飨����Ϊ�ʵ㣩Q�ӹ���ϵ�A���ɾ�ֹ�ͷţ��������D�㣬C��D�ľ���Ϊs���������ٶ�Ϊg�����ƿ��������������� ��1�����Q��A��B�Ĺ��̣����ö��ܶ����������龭��B����ٶȣ���B�㣬��ţ�ٶ��ɺ�������֪ʶ��������Թ����ѹ����
��2������뿪C�����ƽ���˶������ݸ߶Ⱥ�ˮƽ����������龭��C����ٶȣ��ٶԴ�B��C�Ĺ��̣����ö��ܶ������Ħ������������Ĺ���
��3���������Ľ������Ħ������ʽ��Ħ��������
��� �⣺��1����A��B���ɶ��ܶ����ã�mgR=$\frac{1}{2}m{v}_{B}^{2}$-0
��B�㣬��ţ�ٵڶ����ɵã�FN-mg=m$\frac{{v}_{B}^{2}}{R}$
������ã�vB=$\sqrt{2gR}$��FN=3mg
����ţ�ٵ������ɿɵã����Թ����ѹ����СΪ3mg��������ֱ���£�
��2���뿪C�������ƽ���˶���
ˮƽ����s=vCt
��ֱ����h=$\frac{1}{2}$gt2
�����C��Ķ��ܣ�EKC=$\frac{1}{2}$mvC2
��ã�EKC=$\frac{mg{s}^{2}}{4h}$
��B��C�����У��ɶ��ܶ�����Ħ��������Ϊ��Wf=$\frac{1}{2}$mvC2-$\frac{1}{2}$mvB2=$\frac{mg{s}^{2}}{4h}$-mgR
��3����B��C�����У���Wf=-��mgL�ã���=$\frac{R}{L}$-$\frac{{s}^{2}}{4hL}$
�𣺣�1�����Q����B��ʱ�Թ����ѹ����3mg��������ֱ���£�
��2�������Q��B�˶���C�Ĺ����У�Ħ������������Ĺ���$\frac{mg{s}^{2}}{4h}$-mgR��
��3�����Q��ƽ��P֮��Ķ�Ħ��������$\frac{R}{L}$-$\frac{{s}^{2}}{4hL}$��
���� ����ؼ��Ƿ������������˶����ɣ�Ȼ��ֽ�Ӧ�ö��ܶ�����ƽ���˶��ķ��˶�������ʽ��⣬�����ṩ��һ�ֲⶨ��Ħ�������ķ��������Ժ��ʵ������пɹ��ο���


 Ʒѧ˫�ž�ϵ�д�
Ʒѧ˫�ž�ϵ�д� Сѧ��ĩ���100��ϵ�д�
Сѧ��ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �����ʱ��Խ�� | B�� | �����ʱ��Խ�� | C�� | ���ʱ�ٶ�Խ�� | D�� | ���ʱ�ٶ�ԽС |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
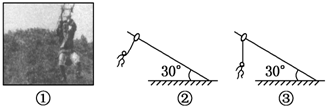
| A�� | ͼ�ڵ������У���ֻ���ȼ����»� | |
| B�� | ͼ�ڵ������У��������ỷ����������СΪ$\frac{\sqrt{3}}{2}$mg | |
| C�� | ͼ�۵������У��������ỷ��Ħ���� | |
| D�� | ͼ�۵������У��������»� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ����С��ijһ�������Сֵ���������� | |
| B�� | ����С���㣬�������� | |
| C�� | һֱ���� | |
| D�� | ����������ijһ���ֵ������С |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ��˥���в����Ħ�������ԭ�Ӻ����������ԭ�Ӻ��������γɵ� | |
| B�� | ���ն�ЧӦ˵������в����� | |
| C�� | ����•�������緢������Ȼ�������� | |
| D�� | �غ��ѱ����˾۱䶼�ᷢ�����������ͷź��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
 ��ͼ��һ�ڱڹ⻬����ֱԲ��������뾶R=0.4m������б��Ϊ60��Ĺ̶�б��������B�㣬Բ������ߵ�Cǡ����Բ��O�����Ϸ�����б������һ���ɣ�һ�˹̶��ڵ����ϣ���һ��������Ϊ0.2kg����飨����Ϊ�ʵ㣩�Ӵ��������ӣ���ѹ������ʹ��鵽A�㣬Ȼ���ͷţ����ǡ�����˶���C�㣮AB��L=$\sqrt{3}$m�������б��Ķ�Ħ��������=$\frac{\sqrt{3}}{3}$��g=10m/s2����
��ͼ��һ�ڱڹ⻬����ֱԲ��������뾶R=0.4m������б��Ϊ60��Ĺ̶�б��������B�㣬Բ������ߵ�Cǡ����Բ��O�����Ϸ�����б������һ���ɣ�һ�˹̶��ڵ����ϣ���һ��������Ϊ0.2kg����飨����Ϊ�ʵ㣩�Ӵ��������ӣ���ѹ������ʹ��鵽A�㣬Ȼ���ͷţ����ǡ�����˶���C�㣮AB��L=$\sqrt{3}$m�������б��Ķ�Ħ��������=$\frac{\sqrt{3}}{3}$��g=10m/s2�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
 �ܳ�ΪL������������Ϊm�Ļ�������һ���������������壬������ˮƽ���ʱ����������Ϊl0����ͼ1��ʾ���ֽ����װ�ͼ2��ֱ���ã���֪����ѹǿΪP0������������ΪS����������֮����Ħ���Ҳ�©���������¶�T0���ֲ��䣬��
�ܳ�ΪL������������Ϊm�Ļ�������һ���������������壬������ˮƽ���ʱ����������Ϊl0����ͼ1��ʾ���ֽ����װ�ͼ2��ֱ���ã���֪����ѹǿΪP0������������ΪS����������֮����Ħ���Ҳ�©���������¶�T0���ֲ��䣬���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
 ij�С������ͼ��װ����֤��е���غ㶨�ɣ�����������������У��Ⱥ�ͨ�������A��B����ʱװ�ò������ͨ��A��B��ʱ��ֱ�ΪtA��tB���ø���ͨ������ŵ�ƽ���ٶȱ�ʾ��������ͨ������ŵ�˲ʱ�ٶȣ����������ż�ľ���Ϊh������ֱ��ΪD�����ص��������ٶ�Ϊg��
ij�С������ͼ��װ����֤��е���غ㶨�ɣ�����������������У��Ⱥ�ͨ�������A��B����ʱװ�ò������ͨ��A��B��ʱ��ֱ�ΪtA��tB���ø���ͨ������ŵ�ƽ���ٶȱ�ʾ��������ͨ������ŵ�˲ʱ�ٶȣ����������ż�ľ���Ϊh������ֱ��ΪD�����ص��������ٶ�Ϊg���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com