
 ①
① m
m ②
② ③
③ m
m ④
④ mv2⑦
mv2⑦ ⑧
⑧

科目:高中物理 来源: 题型:

查看答案和解析>>
科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源:教材完全学案 高中物理必修2(配教科版) 教科版 题型:038
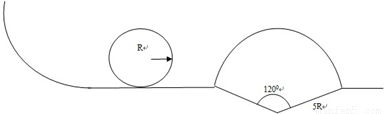
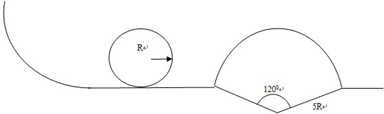
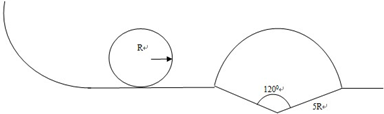
过山车是一项富有刺激性的娱乐工具.那种风驰电掣、有惊无险的快感令不少人着迷.世界上最快的过山车,它的高度h达到了139 m.开始时弹射器将游客乘坐的过山车的车速提高至206 km/h,穿过环形通道,让人有强烈的失重感.如果该游乐场过山车(可视为质点)的运行过程可以抽象为如图所示的模型,弧形轨道的下端与环形轨道相接,使过山车从弧形上端B滑下,进入环形轨道后沿轨道运动,最后离开.已知过山车的质量为1000 kg,R1等于30 m,g取10 m/s2.试求:

(1)要想使过山车获得206 km/h的速度,弹射器至少做多少功?
(2)过山车从A点获得速度后,如果恰好能到达B点,在此过程中克服摩擦力所做的功是多少?这时过山车对轨道的压力有多大?
(3)如果从B到C摩擦力很小,可忽略不计,为了能使过山车通过最高点C,半径R不能大于多少?
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com