
| A. | T=$\frac{{t}_{0}^{2}}{{t}_{0}-{T}_{0}}$ | B. | $R={R_0}\root{3}{{{{(\frac{t_0}{{{t_0}-{T_0}}})}^2}}}$ | ||
| C. | T=$\frac{{t}_{0}}{{t}_{0}-{T}_{0}}$T0 | D. | R=R0$\root{3}{(\frac{{t}_{0}-{T}_{0}}{{t}_{0}})^{2}}$ |
分析 当两行星相距最近时,未知行星对该行星的影响最大,且每隔t0时间相距最近,可知在t0时间内该卫星比未知卫星多运行1圈,结合该关系求出B的周期.由开普勒第三定律求出未知行星的轨道半径
解答 解:AC、行星发生最大偏离时,两行星与恒星在同一直线上且位于恒星同一侧.设未知行星运行周期为T,轨道半径为R,则有:($\frac{2π}{{T}_{0}}$-$\frac{2π}{T}$)t0=2π
解得未知行星的运行周期为:T=$\frac{{t}_{0}}{{t}_{0}-{T}_{0}}$T0,故C正确,A错误.
BD、由开普勒第三定律有:$\frac{{R}_{0}^{3}}{{T}_{0}^{2}}$=$\frac{{T}_{0}^{2}}{{T}^{2}}$,解得:R=R0$\root{3}{(\frac{{t}_{0}}{{t}_{0}-{T}_{0}})^{2}}$,则B正确,D错误
故选:BC
点评 本题考查了万有引力定律的运用,掌握万有引力提供向心力这一理论,并能灵活运用,知道A、B相距最近时,B对A的影响最大,且每隔t0时间相距最近.


 口算题天天练系列答案
口算题天天练系列答案科目:高中物理 来源: 题型:选择题
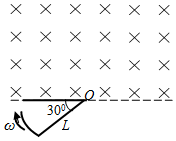 如图所示的区域内有垂直于纸面的匀强磁场,磁感应强度为B.电阻为R、半径为L、圆心角为30°的扇形闭合导线框绕垂直于纸面的o轴以角速度ω匀速转动(o轴位于磁场边界).则线框内产生的感应电流的有效值为( )
如图所示的区域内有垂直于纸面的匀强磁场,磁感应强度为B.电阻为R、半径为L、圆心角为30°的扇形闭合导线框绕垂直于纸面的o轴以角速度ω匀速转动(o轴位于磁场边界).则线框内产生的感应电流的有效值为( )| A. | $\frac{B{L}^{2}ω}{72R}$ | B. | $\frac{\sqrt{6}B{L}^{2}ω}{12R}$ | C. | $\frac{\sqrt{2}B{L}^{2}ω}{4R}$ | D. | $\frac{\sqrt{3}B{L}^{2}ω}{2R}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
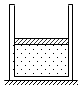 如图所示,内壁光滑、导热良好的汽缸中封闭了一定质量的理想气体,活塞到缸底的距离h=0.5m.已知活塞质量m=2kg,横截面积S=1×10-3m2,环境温度t=0℃且保持不变,外界大气压强p0=1×105Pa,阿伏加德罗常数NA=6×1023mol-1,标准状态下气体的摩尔体积Vmol=22.4L/mol,g=10m/s2.现将汽缸缓慢地转至开口水平,求:
如图所示,内壁光滑、导热良好的汽缸中封闭了一定质量的理想气体,活塞到缸底的距离h=0.5m.已知活塞质量m=2kg,横截面积S=1×10-3m2,环境温度t=0℃且保持不变,外界大气压强p0=1×105Pa,阿伏加德罗常数NA=6×1023mol-1,标准状态下气体的摩尔体积Vmol=22.4L/mol,g=10m/s2.现将汽缸缓慢地转至开口水平,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,下列说法正确的是( )
如图所示,下列说法正确的是( )| A. | 由n=4能级跃迁到n=1能级产生的光子波长最长 | |
| B. | 由n=2能级跃迁到n=1能级产生的光子频率最小 | |
| C. | 这些氢原子总共可辐射出3种不同频率的光 | |
| D. | 用n=2能级跃迁到n=1能级辐射出的光照射逸出功为6.34 eV的金属铂能发生光电效应 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 气体在膨胀时,内能可能不变 | |
| B. | 质量和温度都相同的气体,内能一定相同 | |
| C. | 一定质量的某种理想气体在等压压缩过程中,内能一定减少 | |
| D. | 气体温度不变,整体运动速度越大,其内能越大 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
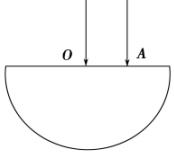 如图所示,半径为R的半圆柱形玻璃砖某一截面的圆心为O点.有两条光线垂直于水平柱面射入玻璃砖中,其中一条光线通过圆心O,另一条光线通过A点,且OA=2R.这两条光线射出玻璃砖后相交于一点,该点到O点的距离为R,求玻璃的折射率.
如图所示,半径为R的半圆柱形玻璃砖某一截面的圆心为O点.有两条光线垂直于水平柱面射入玻璃砖中,其中一条光线通过圆心O,另一条光线通过A点,且OA=2R.这两条光线射出玻璃砖后相交于一点,该点到O点的距离为R,求玻璃的折射率.查看答案和解析>>
科目:高中物理 来源: 题型:多选题
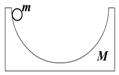 如图所示,质量为M,半径为R的$\frac{1}{2}$光滑圆弧轨道静止于光滑水平面上,质量为m的小球从静止开始自圆弧轨道的左侧最高点滑下,则( )
如图所示,质量为M,半径为R的$\frac{1}{2}$光滑圆弧轨道静止于光滑水平面上,质量为m的小球从静止开始自圆弧轨道的左侧最高点滑下,则( )| A. | m能到达圆弧轨道右侧的最高位置与初始位置等高 | |
| B. | m能到达圆弧轨道右侧的最高位置比初始位置低,不会滑出圆弧轨道 | |
| C. | m能到达圆弧轨道右侧的最高位置比初始位置高,将滑出圆弧轨道 | |
| D. | m到达圆弧轨道右侧最高位置时,M将会向左移动一段位移 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
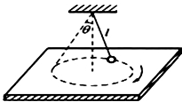 如图所示,长为l的绳子下端连着质量为m的小球,上端悬于天花板上,当绳子拉直时,绳子与竖直方向的夹角为60°,此时,小球静止于光滑水平桌面上,重力加速度为g.则( )
如图所示,长为l的绳子下端连着质量为m的小球,上端悬于天花板上,当绳子拉直时,绳子与竖直方向的夹角为60°,此时,小球静止于光滑水平桌面上,重力加速度为g.则( )| A. | 当小球以角速度ω=$\sqrt{\frac{g}{l}}$做圆锥摆运动时,绳子的张力大小等于重力大小 | |
| B. | 当小球以角速度ω=$\sqrt{\frac{g}{l}}$做圆锥摆运动时,桌面对小球的支持力大小等于重力大小 | |
| C. | 当小球以角速度ω=2$\sqrt{\frac{g}{l}}$做圆锥摆运动时,绳子的张力大小等于重力大小的3倍 | |
| D. | 当小球以角速度ω=$\sqrt{\frac{2g}{l}}$做圆锥摆运动时,桌面对小球恰好没有支持力的作用 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com