
 ��ͼ��ʾ�����߳�Ϊa������Ϊm������ΪR�������ε��߿���ֱ�����׳�����������Ϊb���Ÿ�Ӧǿ��ΪB����ǿ�ų����ų��ķ���ֱֽ������߿������±߸��뿪�ų�ʱ���ٶȸպ����߿��ϱ߸ս���ų�ʱ�ٶȵ�һ�룬�߿��뿪�ų����������һ�θ߶ȣ�Ȼ�����²����ٽ���ų��������˶�������ʼ�մ����Ŵ�С�㶨�Ŀ�������f�����߿���ת������
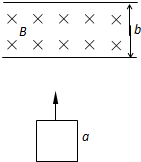
��ͼ��ʾ�����߳�Ϊa������Ϊm������ΪR�������ε��߿���ֱ�����׳�����������Ϊb���Ÿ�Ӧǿ��ΪB����ǿ�ų����ų��ķ���ֱֽ������߿������±߸��뿪�ų�ʱ���ٶȸպ����߿��ϱ߸ս���ų�ʱ�ٶȵ�һ�룬�߿��뿪�ų����������һ�θ߶ȣ�Ȼ�����²����ٽ���ų��������˶�������ʼ�մ����Ŵ�С�㶨�Ŀ�������f�����߿���ת���������� ��1�����������˶����ɹ�������ƽ������������߿���ٶȣ�
��2���ɶ��ܶ���������������ߵ�����ų�˲��ʱ���ٶȣ�����ţ�ٵڶ����ɣ���ϰ���������ʽ������������������ϱ߸ս���ų�ʱ�ļ��ٶȴ�С��
��3����ȫ�̷������������غ㶨�ɿ�����߿��������β����Ľ����ȣ�
��� �⣺��1���߿�����������ٽ���ų�˲����
mg=f+$\frac{{B}^{2}{a}^{2}{v}_{2}}{R}$��
��ã�v2=$\frac{��mg-f��R}{{B}^{2}{a}^{2}}$
�߿�����������ٽ���ų�ʱ���ٶ�$\frac{��mg-f��R}{{B}^{2}{a}^{2}}$��
��2���ɶ��ܶ������߿���뿪�ų�����������ߵ�Ĺ����У�
0-��mg+f��h=0-$\frac{1}{2}$mv12����
��Ȧ����ߵ���������ų�˲�䣺
��mg-f��h=$\frac{1}{2}$mv22����
�ɢ٢ڵã�v1=$\sqrt{\frac{mg+f}{mg-f}}$v2=$\sqrt{��mg��^{2}-{f}^{2}}\frac{R}{{B}^{2}{a}^{2}}$
�߿����������±߸��뿪�ų�ʱ���ٶ�$\sqrt{��mg��^{2}-{f}^{2}}\frac{R}{{B}^{2}{a}^{2}}$��
��ô�߿��ϱ߸ս���ų�ʱ���ٶȵĴ�СΪ��v0=2$\sqrt{��mg��^{2}-{f}^{2}}\frac{R}{{B}^{2}{a}^{2}}$��
����ţ�ٵڶ����ɣ����У�mg+$\frac{{B}^{2}{a}^{2}{v}_{0}}{R}$=ma
��ã�a=g+$\frac{{2B}^{2}{a}^{2}}{mR}$$\sqrt{��mg��^{2}-{f}^{2}}\frac{R}{{B}^{2}{a}^{2}}$��
��3���߿�������ͨ���ų������У��������غ㶨���У�
$\frac{1}{2}$mv02-$\frac{1}{2}$mv12=Q+��mg+f����a+b����v0=2v1
��ã�Q=$\frac{3}{2}$m[��mg��2-f2]$\frac{{R}^{2}}{{B}^{4}{a}^{4}}$-��mg+f����a+b��
�߿���������ͨ���ų������в����Ľ�����Ϊ��Q=$\frac{3}{2}$m[��mg��2-f2]$\frac{{R}^{2}}{{B}^{4}{a}^{4}}$-��mg+f����a+b��
�𣺣�1���߿�����������ٽ���ų�ʱ���ٶ�$\frac{��mg-f��R}{{B}^{2}{a}^{2}}$��
��2���߿����������ϱ߸ս���ų�ʱ�ļ��ٶȴ�Сg+$\frac{{2B}^{2}{a}^{2}}{mR}$$\sqrt{��mg��^{2}-{f}^{2}}\frac{R}{{B}^{2}{a}^{2}}$��
��3���߿���������ͨ���ų������в����ĵ���$\frac{3}{2}$m[��mg��2-f2]$\frac{{R}^{2}}{{B}^{4}{a}^{4}}$-��mg+f����a+b����
���� ��������Ĺؼ�����ȷ���о������˶������ε�����������������������ת�������ѡ������ţ���˶����ɡ����ܶ������ܵ�ת�����غ㶨�ɽ������Ե����⣬���ڹ��̷����������׳��ִ������ԣ������������������е��״��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ԭ������Ȧ������Ϊ5��1 | |
| B�� | ����Ȧ�е�����Ƶ����50Hz | |
| C�� | ԭ��Ȧ�ĵ��߱ȸ���Ȧ��Ҫ�� | |
| D�� | ����ԭ��Ȧ�ĵ������ھ���С�����õ����������ܺ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ���ڹ⻬ˮƽ����Ҳ�����һ�����ֱ����ǿ�糡����ǿ�ų����ų�����ֱֽ��������СΪB�T0.5T�������䷶Χ��������Ϊm=0.1kg�Ľ�������ֹ��ˮƽ���b�㣬��ͬ�ֲ����Ƴɵİ���������������������ͬ���������ٶ�v0=10m/s��ˮƽ�ٶ����������������ײ������ĺ���ǡ����cd�Ҳ�������������Բ���˶�����֪�������������Ϊq=1��10-2C��ȡg=10m/s2����
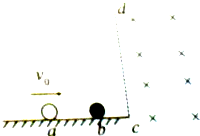
��ͼ��ʾ���ڹ⻬ˮƽ����Ҳ�����һ�����ֱ����ǿ�糡����ǿ�ų����ų�����ֱֽ��������СΪB�T0.5T�������䷶Χ��������Ϊm=0.1kg�Ľ�������ֹ��ˮƽ���b�㣬��ͬ�ֲ����Ƴɵİ���������������������ͬ���������ٶ�v0=10m/s��ˮƽ�ٶ����������������ײ������ĺ���ǡ����cd�Ҳ�������������Բ���˶�����֪�������������Ϊq=1��10-2C��ȡg=10m/s2�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ������������һ������ˮƽ�����˶���С��A��С����װ�е�������B�ĵ�������С��A������B����ͬ��ˮƽ�ٶ�4m/s�ص��۷��������˶���ͬʱ�������������ɾ�ֹ��ʼ��0.5m/s2�ļ��ٶ������ȼ��ٵ��𣬾���6s���������λ�ƺ��ٶȣ�
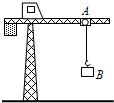
��ͼ������������һ������ˮƽ�����˶���С��A��С����װ�е�������B�ĵ�������С��A������B����ͬ��ˮƽ�ٶ�4m/s�ص��۷��������˶���ͬʱ�������������ɾ�ֹ��ʼ��0.5m/s2�ļ��ٶ������ȼ��ٵ��𣬾���6s���������λ�ƺ��ٶȣ��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
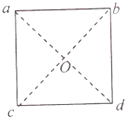 ��ͼ��ʾ��һ�߳�Ϊl�������Σ�����a��b��c���������Ϸֱ�̶��������������ȵ�������Q��O��Ϊ�����ε����ģ�d��Ϊ�����ε���һ�����㣮�����ж���ȷ���ǣ�������
��ͼ��ʾ��һ�߳�Ϊl�������Σ�����a��b��c���������Ϸֱ�̶��������������ȵ�������Q��O��Ϊ�����ε����ģ�d��Ϊ�����ε���һ�����㣮�����ж���ȷ���ǣ�������| A�� | O���d��ij�ǿ������ͬ | |
| B�� | d����Ʊ�O��ĵ��Ƹ� | |
| C�� | ͬһ��̽���+q��d�����O���ܵ��ĵ糡��С | |
| D�� | ͬһ��̽���+q��d�����O��ĵ����ܴ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
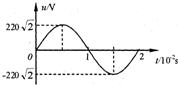
| A�� | �����������������22A | |
| B�� | �ý�����ѹ�������������˵ĵ�ѹ����ʾ��Լ Ϊ311V | |
| C�� | �������ĵĹ���Ϊ9680W | |
| D�� | �ڽ�����仯�İ�������ڣ���������Ľ�������48.4J |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
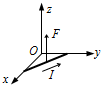 ��ͼ����xOyƽ������һͨ��ֱ������Ox��Oy���ཻ�������е���������ͼ��ʾ������������ǿ�ų���ͨ��ֱ�������ܴų����ķ�����Oz�����������ͬ���ôų��ĴŸ�Ӧǿ�ȵķ�������ǣ�������
��ͼ����xOyƽ������һͨ��ֱ������Ox��Oy���ཻ�������е���������ͼ��ʾ������������ǿ�ų���ͨ��ֱ�������ܴų����ķ�����Oz�����������ͬ���ôų��ĴŸ�Ӧǿ�ȵķ�������ǣ�������| A�� | ��x�������� | B�� | ��y�Ḻ���� | C�� | ��z�������� | D�� | ��z�Ḻ���� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | Ƶ�� | B�� | ���� | C�� | ���� | D�� | ���� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com