
分析 (1)当两车速度相等时,相距最远,结合速度公式和位移公式求出甲乙两车的最大距离.
(2)根据速度时间公式求出甲车速度减为零的时间,结合位移公式求出此时甲、乙的位移,判断乙是否追上,若未追上,结合位移公式求出继续追及的时间,从而得出追及的总时间.
解答 解:(1)当两车速度相等时,相距最远,经历的时间为:$t=\frac{{v}_{乙}-{v}_{甲}}{a}=\frac{9-12}{-2}s=1.5s$,
则最大距离$△x=\frac{{{v}_{乙}}^{2}-{{v}_{甲}}^{2}}{2a}+28-{v}_{乙}t$=$\frac{81-144}{-4}+28-9×1.5m$=30.25m.
(2)甲车速度减为零的时间${t}_{1}=\frac{0-{v}_{甲}}{a}=\frac{-12}{-2}s=6s$,
此时甲车的位移${x}_{甲}=\frac{{{-v}_{甲}}^{2}}{2a}=\frac{-144}{-2×2}m=36m$,
乙车的位移x乙=v乙t1=9×6m=54m,
因为x乙<x甲+28m,可知甲车停止时,乙车还未追上,继续追及的时间:
${t}_{2}=\frac{{x}_{甲}+28-{x}_{乙}}{{v}_{乙}}=\frac{36+28-54}{9}s=\frac{10}{9}s$,
则追及的时间t=${t}_{1}+{t}_{2}=6+\frac{10}{9}s=\frac{64}{9}s$.
答:(1)乙车追上甲车前,甲、乙两车的最大距离是30.25m;
(2)经过$\frac{64}{9}s$时间乙车追上甲车.
点评 此题要注意:乙追上甲车可能有两种不同的情况:甲车停止前被追及和甲车停止后被追及.究竟是哪一种情况,应根据解答结果,有实际情况判断.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案科目:高中物理 来源: 题型:选择题
| A. | $\frac{F}{8}$ | B. | $\frac{F}{4}$ | C. | $\frac{3F}{4}$ | D. | $\frac{3F}{8}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 物体处于超重状态 | B. | 物体处于失重状态 | ||
| C. | 卫星此时的线速度大小为$\frac{\sqrt{2}}{2}$v1 | D. | 卫星此时的线速度大小为$\frac{\sqrt{3}}{3}$v1 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
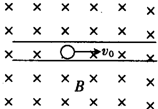 在一绝缘、粗糙且足够长得水平管道中有一带电荷量为q、质量为m的带电球体,管道半径略大于球体半径,整个管道处于磁感应强度为B的水平匀强磁场中,磁感应强度方向与管道垂直.现给带电球体一个水平速度v0,则在整个运动过程中,带电球体克服摩擦力所做的功可能为( )
在一绝缘、粗糙且足够长得水平管道中有一带电荷量为q、质量为m的带电球体,管道半径略大于球体半径,整个管道处于磁感应强度为B的水平匀强磁场中,磁感应强度方向与管道垂直.现给带电球体一个水平速度v0,则在整个运动过程中,带电球体克服摩擦力所做的功可能为( )| A. | 0 | B. | $\frac{1}{2}$mv02 | C. | $\frac{1}{2}$m[v02-($\frac{mg}{qB}$)2] | D. | $\frac{1}{2}$m[v02+($\frac{mg}{qB}$)2] |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 匀速圆周运动是速度大小不变的匀变速曲线运动,速度方向始终为切线方向 | |
| B. | 牛顿发现了万有引力定律,库伦用扭秤实验测出了万有引力恒量的数值 | |
| C. | 根据开普勒第二定律可知北半球夏季比冬季线速度小 | |
| D. | 行星绕恒星运动轨道为圆形,则它运动的周期平方与轨道半径的三次方之比$\frac{T^2}{R^3}=K$为常数,此常数的大小与恒星的质量和行星的速度有关 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
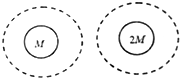 科学家预测银河系中所有行星的数量大概为2万亿-3万亿之间,若宇宙中有一颗未知行星,其半径和地球半径相同,但质量却是地球质量的两倍,如地球上的卫星a和未知行星上的卫星b距离地面的距离相同,则( )
科学家预测银河系中所有行星的数量大概为2万亿-3万亿之间,若宇宙中有一颗未知行星,其半径和地球半径相同,但质量却是地球质量的两倍,如地球上的卫星a和未知行星上的卫星b距离地面的距离相同,则( )| A. | 卫星a和卫星b的线速度之比为$\frac{1}{\sqrt{2}}$ | |
| B. | 卫星a和卫星b的线速度之比为$\frac{1}{\sqrt{8}}$ | |
| C. | 卫星a和卫星b的周期之比为$\sqrt{2}$:1 | |
| D. | 卫星a和卫星b的向心加速度之比为1:2 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
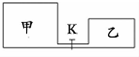 如图所示,装有同种理想气体的甲乙两个容器之间由细管相连.开始时阀门k关闭.甲中气体的体积为2V,压强为3P,温度为T,乙中气体的体积为V,压强为P,温度为T.现打开阀门,直至达到重新平衡,且温度保持不变.求:
如图所示,装有同种理想气体的甲乙两个容器之间由细管相连.开始时阀门k关闭.甲中气体的体积为2V,压强为3P,温度为T,乙中气体的体积为V,压强为P,温度为T.现打开阀门,直至达到重新平衡,且温度保持不变.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com